题目内容
16. 如图,△ABC中,AB=AC,点D在AC边上,且BD=BC=AD,则∠A的度数为( )
如图,△ABC中,AB=AC,点D在AC边上,且BD=BC=AD,则∠A的度数为( )| A. | 30° | B. | 36° | C. | 45° | D. | 70° |
分析 利用等边对等角得到三对角相等,设∠A=∠ABD=x,表示出∠BDC与∠C,列出关于x的方程,求出方程的解得到x的值,即可确定出∠A的度数.
解答 解:∵AB=AC,
∴∠ABC=∠C,
∵BD=BC=AD,
∴∠A=∠ABD,∠C=∠BDC,
设∠A=∠ABD=x,则∠BDC=2x,∠C=$\frac{180°-x}{2}$,
可得2x=$\frac{180°-x}{2}$,
解得:x=36°,
则∠A=36°,
故选B
点评 此题考查了等腰三角形的性质,以及三角形内角和定理,熟练掌握等腰三角形的性质是解本题的关键.

练习册系列答案
相关题目
11.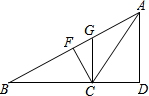 如图,AD⊥BC于点D,GC⊥BC于点C,CF⊥AB于点F,下列关于高的说法中错误的是( )
如图,AD⊥BC于点D,GC⊥BC于点C,CF⊥AB于点F,下列关于高的说法中错误的是( )
 如图,AD⊥BC于点D,GC⊥BC于点C,CF⊥AB于点F,下列关于高的说法中错误的是( )
如图,AD⊥BC于点D,GC⊥BC于点C,CF⊥AB于点F,下列关于高的说法中错误的是( )| A. | △ABC中,AD是BC边上的高 | B. | △GBC中,CF是BG边上的高 | ||
| C. | △ABC中,GC是BC边上的高 | D. | △GBC中,GC是BC边上的高 |
6.如图的几何体中,其主视图为三角形的是( )
| A. |  | B. |  | C. |  | D. |  |
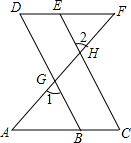 如图,已知AF分别交BD、CE于G、H,∠A=∠F,∠C=∠D.
如图,已知AF分别交BD、CE于G、H,∠A=∠F,∠C=∠D.