题目内容
2.若等式x2+px+q=(x+1)(x-3)成立,则p+q=-5.分析 已知等式左边利用多项式乘以多项式法则计算,再利用多项式相等的条件求出p与q的值,即可求出原式的值.
解答 解:已知等式整理得:x2+px+q=(x+1)(x-3)=x2-2x-3,
可得p=-2,q=-3,
则p+q=-5,
故答案为:-5
点评 此题考查了因式分解-十字相乘法,以及多项式的乘法,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.下列运算结果正确的是( )
| A. | a2+a3=a5 | B. | a3÷a2=a | C. | a2•a3=a6 | D. | (a2)3=a5 |
13.下列命题正确的是( )
| A. | 对角线互相垂直的四边形是菱形 | |
| B. | 对角线相等且垂直的四边形是正方形 | |
| C. | 平行四边形的对角线互相平分 | |
| D. | 对角线相等的四边形是矩形 |
14.小明的讲义夹里放了大小相同的试卷共12页,其中语文4页,数学2页,英语6页,他随机地从讲义夹中抽出1页,抽出的试卷恰好是数学试卷的概率为( )
| A. | $\frac{1}{12}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{6}$ |
 如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是( )
如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是( )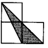



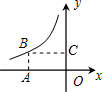 如图,矩形OABC上,点A、C分别在x、y轴上,点B在反比例y=$\frac{k}{x}$位于第二象限的图象上,矩形面积为6,则k的值是( )
如图,矩形OABC上,点A、C分别在x、y轴上,点B在反比例y=$\frac{k}{x}$位于第二象限的图象上,矩形面积为6,则k的值是( )