题目内容
11.解关于x,y,z的方程组:$\left\{\begin{array}{l}{2x-y=0}\\{x-z-1=0}\\{x+yz-3=0}\end{array}\right.$.分析 由①得出y=2x,由②得出z=x-1,代入③得出x+2x(x-1)-3=0,求出x,再求出y、z即可.
解答 解:$\left\{\begin{array}{l}{2x-y=0①}\\{x-z-1=0②}\\{x+yz-3=0③}\end{array}\right.$
由①得:y=2x④,
由②得:z=x-1⑤,
把④⑤代入③得:x+2x(x-1)-3=0,
解得:x=$\frac{3}{2}$或-1,
当x=$\frac{3}{2}$时,y=3,z=$\frac{1}{2}$,
当x=-1时,y=-2,z=-2,
所以原方程组的解为:$\left\{\begin{array}{l}{x=\frac{3}{2}}\\{y=3}\\{z=\frac{1}{2}}\\{\;}\end{array}\right.$,$\left\{\begin{array}{l}{x=-1}\\{y=-2}\\{z=-2}\end{array}\right.$.
点评 本题考查了解三元方程组,能把三元方程组转化成一元二次方程是解此题的关键.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
19.为了调查瑞州市2016年初三年级学生的身高,从中抽取出200名学生进行调查,这个问题中样本容量为( )
| A. | 被抽取的200名学生的身高 | B. | 200 | ||
| C. | 200名 | D. | 初三年级学生的身高 |
6.下列说法正确的是( )
| A. | 随机抛掷一枚硬币,反面一定朝上 | |
| B. | 数据3,3,5,5,8的众数是8 | |
| C. | 某商场抽奖活动获奖的概率为$\frac{1}{50}$,说明毎买50张奖券中一定有一张中奖 | |
| D. | 想要了解广安市民对“全面二孩”政策的看法,宜采用抽样调查 |
16.已知二次函数y=(x-h)2+1(h为常数),在自变量x的值满足1≤x≤3的情况下,与其对应的函数值y的最小值为5,则h的值是( )
| A. | 1或-5 | B. | 1或3 | C. | 1或-3 | D. | -1或5 |
1.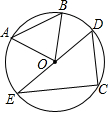 如图,已知AB,CD是⊙O的弦,且AB=CD,∠AOB=70°,则∠CED的度数为( )
如图,已知AB,CD是⊙O的弦,且AB=CD,∠AOB=70°,则∠CED的度数为( )
 如图,已知AB,CD是⊙O的弦,且AB=CD,∠AOB=70°,则∠CED的度数为( )
如图,已知AB,CD是⊙O的弦,且AB=CD,∠AOB=70°,则∠CED的度数为( )| A. | 70° | B. | 60° | C. | 45° | D. | 35° |
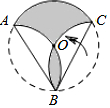 如图,将半径为6的圆形纸片,分别沿AB、BC折叠,若弧AB和弧BC折后都经过圆心O,则阴影部分的面积是12π(结果保留π)
如图,将半径为6的圆形纸片,分别沿AB、BC折叠,若弧AB和弧BC折后都经过圆心O,则阴影部分的面积是12π(结果保留π) 若m,n为正实数,t是关于x的方程x2+2mx=n2的一正实数根,
若m,n为正实数,t是关于x的方程x2+2mx=n2的一正实数根, 如图,梯形ABCD中,AD∥BC,AD:BC=1:3,对角线AC与BD相交于点O,AE⊥BC,垂足为E,AE恰好过BD的中点F,∠FBE=30°
如图,梯形ABCD中,AD∥BC,AD:BC=1:3,对角线AC与BD相交于点O,AE⊥BC,垂足为E,AE恰好过BD的中点F,∠FBE=30°