题目内容
 已知:如图,梯形ABCD中,AD∥BC,AD+BC=20,M是AB的中点,MD⊥DC,D是垂足,sinC=
已知:如图,梯形ABCD中,AD∥BC,AD+BC=20,M是AB的中点,MD⊥DC,D是垂足,sinC=| 4 |
| 5 |
考点:梯形,解直角三角形
专题:
分析:用作辅助线的方法把梯形的上底移到下底上,从而梯形的面积转化成三角形的面积来解决.
解答: 解:延长DM交CB的延长线于点E,
解:延长DM交CB的延长线于点E,
∵AD∥CE,∴∠ADM=∠E,
∵M是AB的中点,
∴AM=BM,
在△ADM与△BEM中,
,
∴△ADM≌△BEM(ASA),
∴AD=BE.
∵AD+BC=20,
∴EB+BC=20,即CE=20,
∵MD⊥DC,
∴∠CDE=90°,
∵sin∠C=
,
∴
=
,
∴DE=16.由勾股定理得CD=
=
=12,
∴S梯形ABCD=S△CDE=
DE•DC=
×16×12=96.
 解:延长DM交CB的延长线于点E,
解:延长DM交CB的延长线于点E,∵AD∥CE,∴∠ADM=∠E,
∵M是AB的中点,
∴AM=BM,
在△ADM与△BEM中,
|
∴△ADM≌△BEM(ASA),
∴AD=BE.
∵AD+BC=20,
∴EB+BC=20,即CE=20,
∵MD⊥DC,
∴∠CDE=90°,
∵sin∠C=
| 4 |
| 5 |
∴
| DE |
| EC |
| 4 |
| 5 |
∴DE=16.由勾股定理得CD=
| CE2-DE2 |
| 202-162 |
∴S梯形ABCD=S△CDE=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查的是梯形和解直角三角形,需要用到梯形的面积转化成三角形的面积.

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目

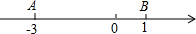 已知:如图数轴上两动点A、B原始位置所对应的数分别为-3、1,
已知:如图数轴上两动点A、B原始位置所对应的数分别为-3、1, 如图,在△ADF和△BCE中,点D、E、F、C在同一直线上,AF∥BE,AF=BE,DE=CF.求证:∠A=∠B.
如图,在△ADF和△BCE中,点D、E、F、C在同一直线上,AF∥BE,AF=BE,DE=CF.求证:∠A=∠B. 如图,在10×10正方形网格中,每个小正方形的边长均为1个单位.将△ABC关于x轴对称,得到△A′B′C′,再把△A′B′C′关于y轴对称,得到△A′B′C′,请你画出△A′B′C′和△A″B″C″.(不要求写画法)
如图,在10×10正方形网格中,每个小正方形的边长均为1个单位.将△ABC关于x轴对称,得到△A′B′C′,再把△A′B′C′关于y轴对称,得到△A′B′C′,请你画出△A′B′C′和△A″B″C″.(不要求写画法)