题目内容
16.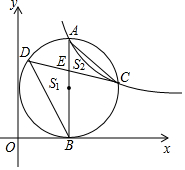 如图,点A是反比例函数y=$\frac{k}{x}$(k>0)图象第一象限上一点,过点A作AB⊥x轴于B点,以AB为直径的圆恰好与y轴相切,交反比例函数图象于点C,在AB的左侧半圆上有一动点D,连结CD交AB于点E.记△BDE的面积为S1,△ACE的面积为S2,若S1-S2的值最大为1,则k的值为4$\sqrt{2}$+4.
如图,点A是反比例函数y=$\frac{k}{x}$(k>0)图象第一象限上一点,过点A作AB⊥x轴于B点,以AB为直径的圆恰好与y轴相切,交反比例函数图象于点C,在AB的左侧半圆上有一动点D,连结CD交AB于点E.记△BDE的面积为S1,△ACE的面积为S2,若S1-S2的值最大为1,则k的值为4$\sqrt{2}$+4.
分析 如图连接BC、O′C,作CH⊥x轴于H.首先证明四边形BHCO′是正方形.推出∠ABC=45°,推出△ACB是等腰直角三角形,由S1-S2=S△DBC-S△ACB,△ABC的面积是定值,推出△DBC的面积最大时,S1-S2的值最大,推出当DO′⊥BC时,△DBC 的面积最大,可得$\frac{1}{2}$•$\sqrt{2}$m•(m+$\frac{\sqrt{2}}{2}$m)-$\frac{1}{2}$•2m•m=1,解方程即可解决问题.
解答 解:如图连接BC、O′C,作CH⊥x轴于H.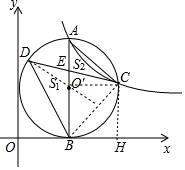
由题意⊙O′与反比例函数图象均关于直线y=x对称,
∴点A、C关于直线y=x对称,设A(m,2m)则C(2m,m),
∴BO′=CH=m,BO′∥CH,
∴四边形BHCO′是平行四边形,∵BH=CH,∠BHC=90°,
∴四边形BHCO′是正方形.
∴∠ABC=45°,
∴△ACB是等腰直角三角形,
∵S1-S2=S△DBC-S△ACB,△ABC的面积是定值,
∴△DBC的面积最大时,S1-S2的值最大,
∴当DO′⊥BC时,△DBC 的面积最大,
∴$\frac{1}{2}$•$\sqrt{2}$m•(m+$\frac{\sqrt{2}}{2}$m)-$\frac{1}{2}$•2m•m=1,
∴m2=2($\sqrt{2}$+1),
∵k=2m2,
∴k=4$\sqrt{2}$+4,
故答案为4$\sqrt{2}$+4.
点评 本题考查反比例函数综合题、圆的有关性质、正方形的性质、等腰直角三角形的性质、轴对称的性质等知识,解题的关键是学会添加辅助线,构造特殊四边形解决问题,学会用转化的思想思考问题,属于中考常考题型.

练习册系列答案
相关题目
11.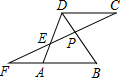 如图,点P是菱形ABCD对角线BD上一点,连接CP并延长,交AD于点E,交BA的延长线于点F,则线段PC、PE、PF之间存在的数量关系是( )
如图,点P是菱形ABCD对角线BD上一点,连接CP并延长,交AD于点E,交BA的延长线于点F,则线段PC、PE、PF之间存在的数量关系是( )
 如图,点P是菱形ABCD对角线BD上一点,连接CP并延长,交AD于点E,交BA的延长线于点F,则线段PC、PE、PF之间存在的数量关系是( )
如图,点P是菱形ABCD对角线BD上一点,连接CP并延长,交AD于点E,交BA的延长线于点F,则线段PC、PE、PF之间存在的数量关系是( )| A. | 2PC=PE+PF | B. | 2PC=PE•PF | C. | PC2=PE•PF | D. | PC2=$\frac{PF}{PE}$ |
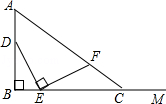 如图,AB=4,射线BM和AB互相垂直,点D是AB上的一个动点,点E在射线BM上,BE=$\frac{1}{2}$DB,作EF⊥DE,并截取EF=DE,连接AF并延长交射线BM于点C,设BE=x,BC=y,则y关于x的函数解析式为y=$\frac{12x}{4-x}$(0<x≤2).
如图,AB=4,射线BM和AB互相垂直,点D是AB上的一个动点,点E在射线BM上,BE=$\frac{1}{2}$DB,作EF⊥DE,并截取EF=DE,连接AF并延长交射线BM于点C,设BE=x,BC=y,则y关于x的函数解析式为y=$\frac{12x}{4-x}$(0<x≤2).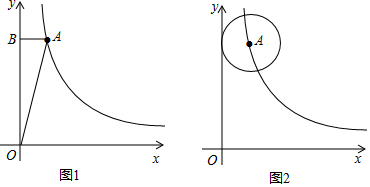
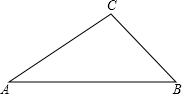 已知:如图,在△ABC中,∠ABC=45°,tanA=$\frac{3}{4}$,AB=14,
已知:如图,在△ABC中,∠ABC=45°,tanA=$\frac{3}{4}$,AB=14,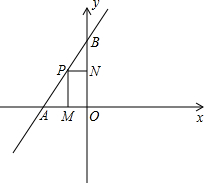 如图,在平面直角坐标系中,直线y=$\frac{3}{2}$x+6与x轴交于点A,与y轴交于点B,P为线段AB上一动点(不与A,B两点重合),过点P作PM⊥x轴,PN⊥y轴,垂足分别为M,N.设OM=a,四边形PMON面积为s.
如图,在平面直角坐标系中,直线y=$\frac{3}{2}$x+6与x轴交于点A,与y轴交于点B,P为线段AB上一动点(不与A,B两点重合),过点P作PM⊥x轴,PN⊥y轴,垂足分别为M,N.设OM=a,四边形PMON面积为s.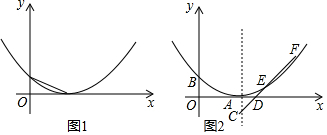
 (1)我们知道,将一条线段AB分割成大小两条线段AP、PB,使AP>PB,点P把线段AB分成两条线段AP和BP,且$\frac{AP}{AB}$=$\frac{BP}{AP}$,点P就是线段AB的黄金分割点,此时$\frac{PA}{AB}$的值为$\frac{\sqrt{5}-1}{2}$ (填一个实数):
(1)我们知道,将一条线段AB分割成大小两条线段AP、PB,使AP>PB,点P把线段AB分成两条线段AP和BP,且$\frac{AP}{AB}$=$\frac{BP}{AP}$,点P就是线段AB的黄金分割点,此时$\frac{PA}{AB}$的值为$\frac{\sqrt{5}-1}{2}$ (填一个实数):