题目内容
4.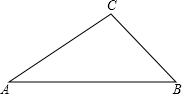 已知:如图,在△ABC中,∠ABC=45°,tanA=$\frac{3}{4}$,AB=14,
已知:如图,在△ABC中,∠ABC=45°,tanA=$\frac{3}{4}$,AB=14,(1)求:△ABC的面积;
(2)若以C为圆心的圆C与直线AB相切,以A为圆心的圆A与圆C相切,试求圆A的半径.
分析 (1)过C作CD⊥AB于D,解直角三角形得到CD=$\frac{45}{7}$,根据三角形的面积公式即可得到结论;
(2)根据圆C与直线AB相切,得到⊙C的半径=$\frac{45}{7}$,根据勾股定理得到AC=$\sqrt{C{D}^{2}+A{D}^{2}}$=$\frac{75}{7}$,设⊙A的半径为r,当圆A与圆C内切时,当圆A与圆C外切时即可得到结论.
解答 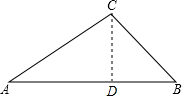 解:(1)过C作CD⊥AB于D,
解:(1)过C作CD⊥AB于D,
∵tanA=$\frac{CD}{AD}$=$\frac{3}{4}$,
∴AD=$\frac{4CD}{3}$,
∵∠ABC=45°,
∴BD=CD,
∵AB=14,
∴$\frac{4CD}{3}$+CD=15,
∴CD=$\frac{45}{7}$,
∴△ABC的面积=$\frac{1}{2}$AB•CD=$\frac{1}{2}$×15×$\frac{45}{7}$=$\frac{675}{14}$;
(2)∵以C为圆心的圆C与直线AB相切,
∴⊙C的半径=$\frac{45}{7}$,
∵AD=$\frac{60}{7}$,
∴AC=$\sqrt{C{D}^{2}+A{D}^{2}}$=$\frac{75}{7}$,
设⊙A的半径为r,
当圆A与圆C内切时,r-$\frac{45}{7}$=$\frac{75}{7}$,
∴r=$\frac{120}{7}$,
当圆A与圆C外切时,r+$\frac{45}{7}$=$\frac{75}{7}$,
∴r=$\frac{30}{7}$,
综上所述:以A为圆心的圆A与圆C相切,圆A的半径为:$\frac{120}{7}$或$\frac{30}{7}$.
点评 本题考查了圆与圆的位置关系,勾股定理,三角形的面积的计算,解直角三角形,注意分类讨论思想的应用.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案| A. | 1 | B. | $\frac{3}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
| A. | m4•m5=m9 | B. | 5x-7x=-2x | ||
| C. | (-x)5÷(-x)2=-x3 | D. | $\frac{{a}^{2}+4a+4}{-{a}^{2}+4}$=$\frac{a+2}{a-2}$ |
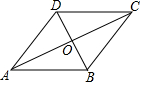 如图,平行四边形ABCD的对角线AC,BD相交于点O,补充下面一个条件,不能判定平行四边形ABCD是菱形的是( )
如图,平行四边形ABCD的对角线AC,BD相交于点O,补充下面一个条件,不能判定平行四边形ABCD是菱形的是( )| A. | AB=BC | B. | AO=BO | C. | ∠DOC=90° | D. | ∠CDO=∠ADO |
| 应试者 | 听 | 说 | 读 | 写 |
| 甲 | 85 | 78 | 85 | 73 |
| 乙 | 73 | 80 | 82 | 83 |
(2)如果这家公司想招一名笔译能力较强,听、说、读、写成绩按照2:1:3:4的比确定,计算两名应试者的平均成绩(百分制).从他们的成绩看,应该录取谁?
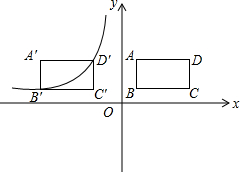 如图所示,在平面直角坐标系中,矩形ABCD,AB=2,BC=4,点B(1,1).
如图所示,在平面直角坐标系中,矩形ABCD,AB=2,BC=4,点B(1,1).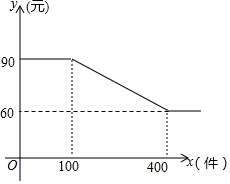 某衬衫厂生产某品牌衬衫的成本价为50元/件,批发价y元/件与一次性批发件数x件之间的关系满足图中折线的函数关系,批发件数为10的正整数倍.
某衬衫厂生产某品牌衬衫的成本价为50元/件,批发价y元/件与一次性批发件数x件之间的关系满足图中折线的函数关系,批发件数为10的正整数倍.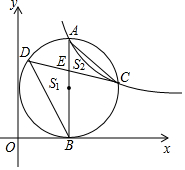 如图,点A是反比例函数y=$\frac{k}{x}$(k>0)图象第一象限上一点,过点A作AB⊥x轴于B点,以AB为直径的圆恰好与y轴相切,交反比例函数图象于点C,在AB的左侧半圆上有一动点D,连结CD交AB于点E.记△BDE的面积为S1,△ACE的面积为S2,若S1-S2的值最大为1,则k的值为4$\sqrt{2}$+4.
如图,点A是反比例函数y=$\frac{k}{x}$(k>0)图象第一象限上一点,过点A作AB⊥x轴于B点,以AB为直径的圆恰好与y轴相切,交反比例函数图象于点C,在AB的左侧半圆上有一动点D,连结CD交AB于点E.记△BDE的面积为S1,△ACE的面积为S2,若S1-S2的值最大为1,则k的值为4$\sqrt{2}$+4.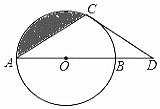 如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,⊙O的半径为3,$\widehat{BC}$的长为π.
如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,⊙O的半径为3,$\widehat{BC}$的长为π.