题目内容
11.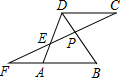 如图,点P是菱形ABCD对角线BD上一点,连接CP并延长,交AD于点E,交BA的延长线于点F,则线段PC、PE、PF之间存在的数量关系是( )
如图,点P是菱形ABCD对角线BD上一点,连接CP并延长,交AD于点E,交BA的延长线于点F,则线段PC、PE、PF之间存在的数量关系是( )| A. | 2PC=PE+PF | B. | 2PC=PE•PF | C. | PC2=PE•PF | D. | PC2=$\frac{PF}{PE}$ |
分析 根据菱形的性质得∠ADP=∠CDP,DA=DC,从而得到△APD与△CPD全等,根据全等三角形的性质得到∠DCP=∠DAP,根据菱形的对边互相平行得∠DCF=∠F,从而证得△PAE∽△PFA,然后利用比例线段证得等积式即可.
解答 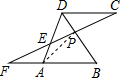 解:∵四边形ABCD为菱形,
解:∵四边形ABCD为菱形,
∴∠ADP=∠CDP,DC=DA,
在△APD和△CPD中,$\left\{\begin{array}{l}{DC=DA}\\{∠ADP=∠CDP}\\{DP=DP}\end{array}\right.$,
∴△APD≌△CPD(SAS);
∴PA=PC,∠DCP=∠DAP,
∵四边形ABCD为菱形,
∴∠DCF=∠F,
∴∠F=∠PAE,
∴△PAE∽△PFA,
∴$\frac{PA}{PE}=\frac{PF}{PA}$,
即:PA2=PE•PF,
∴PC2=PE•PF.
故选C.
点评 本题考查了菱形的性质、全等三角形的判定及相似三角形的判定及性质,是一道不错的综合题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
20.甲、乙两商场以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购物超过100元后,超出100元的部分按90%收费;在乙商场累计购物超过50元后,超出50元的部分按95%收费,设小红在同一商场累计购物x元,其中x>100.
(1)根据题题意,填写表格(单位:元)
(2)设小红在甲、乙两商场的实际花费分别为y1元、y2元,请分别写出y1、y2与x之间的关系式?
(3)小红选择哪家商场购物更合算?
(1)根据题题意,填写表格(单位:元)
| 累计购物 | 130 | 250 | … |
| 在甲商场 实际花费 | 100+(130-100)×90% | 100+(250-100)×90% | … |
| 在乙商场 实际花费 | 50+(130-50)×95% | 50+(250-50)×95% | … |
(3)小红选择哪家商场购物更合算?
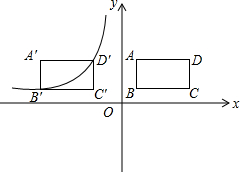 如图所示,在平面直角坐标系中,矩形ABCD,AB=2,BC=4,点B(1,1).
如图所示,在平面直角坐标系中,矩形ABCD,AB=2,BC=4,点B(1,1).



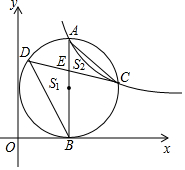 如图,点A是反比例函数y=$\frac{k}{x}$(k>0)图象第一象限上一点,过点A作AB⊥x轴于B点,以AB为直径的圆恰好与y轴相切,交反比例函数图象于点C,在AB的左侧半圆上有一动点D,连结CD交AB于点E.记△BDE的面积为S1,△ACE的面积为S2,若S1-S2的值最大为1,则k的值为4$\sqrt{2}$+4.
如图,点A是反比例函数y=$\frac{k}{x}$(k>0)图象第一象限上一点,过点A作AB⊥x轴于B点,以AB为直径的圆恰好与y轴相切,交反比例函数图象于点C,在AB的左侧半圆上有一动点D,连结CD交AB于点E.记△BDE的面积为S1,△ACE的面积为S2,若S1-S2的值最大为1,则k的值为4$\sqrt{2}$+4.