题目内容
6.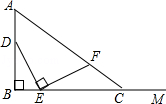 如图,AB=4,射线BM和AB互相垂直,点D是AB上的一个动点,点E在射线BM上,BE=$\frac{1}{2}$DB,作EF⊥DE,并截取EF=DE,连接AF并延长交射线BM于点C,设BE=x,BC=y,则y关于x的函数解析式为y=$\frac{12x}{4-x}$(0<x≤2).
如图,AB=4,射线BM和AB互相垂直,点D是AB上的一个动点,点E在射线BM上,BE=$\frac{1}{2}$DB,作EF⊥DE,并截取EF=DE,连接AF并延长交射线BM于点C,设BE=x,BC=y,则y关于x的函数解析式为y=$\frac{12x}{4-x}$(0<x≤2).
分析 作FM⊥BC于M.由△DBE≌△EMF,推出FM=BE=x,EM=BD=2BE=2x,由FM∥AB,推出$\frac{FM}{AB}$=$\frac{CM}{CB}$,即$\frac{x}{4}$=$\frac{y-3x}{y}$,由此即可解决问题.
解答 解:作FM⊥BC于M.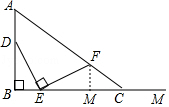
∵∠DBE=∠DEF=∠EMF=90°,
∴∠DEB+∠BDE=90°,∠DEB+∠FEM=90°,
∴∠BDE=∠FEM.
在△DBE和△EMF中,
$\left\{\begin{array}{l}{∠BDE=∠FEM}\\{∠B=∠EMF}\\{DE=EF}\end{array}\right.$,
∴△DBE≌△EMF,
∴FM=BE=x,EM=BD=2BE=2x,
∵FM∥AB,
∴$\frac{FM}{AB}$=$\frac{CM}{CB}$,
∴$\frac{x}{4}$=$\frac{y-3x}{y}$,
∴y=$\frac{12x}{4-x}$(0<x≤2).
点评 本题考查全等三角形的判定和性质、平行线分线段成比例定理等知识,解题的关键是灵活应用所学知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
17.上学期期末考试,某小组五位同学的数学成绩分别是90,113,102,90,98,则这五个数据的中位数是( )
| A. | 90 | B. | 98 | C. | 100 | D. | 105 |
14.将一边长为2的正方形纸片折成四部分,再沿折痕折起来,恰好能不重叠地围成一个三棱锥,则这个三棱锥四个面中最大的面积等于( )
| A. | 1 | B. | $\frac{3}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
15.下列计算不正确的是( )
| A. | m4•m5=m9 | B. | 5x-7x=-2x | ||
| C. | (-x)5÷(-x)2=-x3 | D. | $\frac{{a}^{2}+4a+4}{-{a}^{2}+4}$=$\frac{a+2}{a-2}$ |
 阅读材料
阅读材料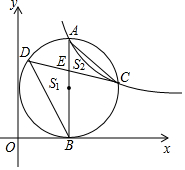 如图,点A是反比例函数y=$\frac{k}{x}$(k>0)图象第一象限上一点,过点A作AB⊥x轴于B点,以AB为直径的圆恰好与y轴相切,交反比例函数图象于点C,在AB的左侧半圆上有一动点D,连结CD交AB于点E.记△BDE的面积为S1,△ACE的面积为S2,若S1-S2的值最大为1,则k的值为4$\sqrt{2}$+4.
如图,点A是反比例函数y=$\frac{k}{x}$(k>0)图象第一象限上一点,过点A作AB⊥x轴于B点,以AB为直径的圆恰好与y轴相切,交反比例函数图象于点C,在AB的左侧半圆上有一动点D,连结CD交AB于点E.记△BDE的面积为S1,△ACE的面积为S2,若S1-S2的值最大为1,则k的值为4$\sqrt{2}$+4.