题目内容
7.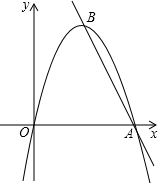 如图,抛物线y=ax2+bx与x轴的正半轴交于点A,抛物线的顶点为B,且点B的纵坐标为6,直线y=kx-6k经过A、B两点.
如图,抛物线y=ax2+bx与x轴的正半轴交于点A,抛物线的顶点为B,且点B的纵坐标为6,直线y=kx-6k经过A、B两点.(1)求抛物线的解析式;
(2)点C在抛物线上,使得S△ABC=10,求点C的坐标.
分析 (1)先求出一次函数与x轴的交点A的坐标(6,0),则可得到顶点B的坐标为(3,6),设顶点式y=a(x-3)2+6,然后把A点代入求出a即可得到抛物线解析式;
(2)作BD⊥x轴于D,CE⊥x轴于E,如图,设C(x,-$\frac{2}{3}$x2+4x),利用S△ABC=S梯形BDEC+S△ABD-S△ACE得到x2-3x-9=10,然后解方程求出x即可得到C点坐标.
解答 解:(1)当y=0时,kx-6k=0,解得x=6,则A(6,0),
∴抛物线的对称轴为直线x=3,
∴顶点B的坐标为(3,6),
设抛物线的解析式为y=a(x-3)2+6,
把A(6,0)代入得a(6-3)2+6=0,解得a=-$\frac{2}{3}$,
∴抛物线的解析式为y=-$\frac{2}{3}$(x-3)2+6,即y=-$\frac{2}{3}$x2+4x;
(2)作BD⊥x轴于D,CE⊥x轴于E,如图,
设C(x,-$\frac{2}{3}$x2+4x)
∵S△ABC=S梯形BDEC+S△ABD-S△ACE=$\frac{1}{2}$(-$\frac{2}{3}$x2+4x+6)•(3-x)+$\frac{1}{2}$•6•3-$\frac{1}{2}$(-$\frac{2}{3}$x2+4x+6)•(6-x)=x2-3x-9,
∴x2-3x-9=10,解得x1=$\frac{3+\sqrt{85}}{2}$,x2=$\frac{3-\sqrt{85}}{2}$,
∴点C的纵坐标为($\frac{3+\sqrt{85}}{2}$,$\frac{-29+3\sqrt{85}}{3}$)或($\frac{3-\sqrt{85}}{2}$,$\frac{-29+3\sqrt{85}}{3}$).
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化解关于x的一元二次方程.也考查了一次函数的性质.

| A. | 400元,600元 | B. | 600元,400元 | C. | 580元,440元 | D. | 520元,460元 |
| A. | 3x+7x=1 | B. | $\frac{x}{3}$+$\frac{x}{7}$=1 | C. | ($\frac{1}{3}$-$\frac{1}{7}$)x=1 | D. | x=($\frac{1}{3}$-$\frac{1}{7}$)-1 |
| A. | (4,-3) | B. | (4,3) | C. | (-4,3) | D. | (-4,-3) |
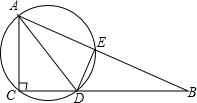 如图,在Rt△ABC中,∠ACB=90,AD平分∠BAC,过A,C,D三点的圆与斜边AB交于点E,连接DE.
如图,在Rt△ABC中,∠ACB=90,AD平分∠BAC,过A,C,D三点的圆与斜边AB交于点E,连接DE.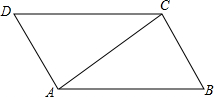 如图,AC是平行四边形ABCD的对角线.
如图,AC是平行四边形ABCD的对角线.