题目内容
17.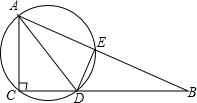 如图,在Rt△ABC中,∠ACB=90,AD平分∠BAC,过A,C,D三点的圆与斜边AB交于点E,连接DE.
如图,在Rt△ABC中,∠ACB=90,AD平分∠BAC,过A,C,D三点的圆与斜边AB交于点E,连接DE.(1)求证:AC=AE;
(2)若AC=6,CB=8,求△ACD的外接圆的直径.
分析 (1)根据角平分线的性质、圆周角、弧、弦之间的关系得到$\widehat{AC}$=$\widehat{AE}$,证明结论;
(2)根据勾股定理求出AB,设CD=DE=x,根据勾股定理列出方程,求出x,计算即可.
解答 (1)证明:∵AD平分∠BAC,
∴∠CAD=∠EAD,
∴$\widehat{CD}$=$\widehat{ED}$,
∴CD=ED
∵∠ACD=90°,
∴AD是⊙O的直径,
∴$\widehat{AC}$=$\widehat{AE}$,
∴AC=AE;
(2)在Rt△ABC中,∠ACB=90°,AC=6,BC=8,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=10,
BE=10-AE=10-6=4,
设CD=DE=x,
BD=8-x,
在Rt△BDE中.BD2=DE2+BE2
(8-x)2+x2=42
x=3,即BD=3,
在Rt△ACD中,AD=$\sqrt{A{C}^{2}+C{D}^{2}}$=3$\sqrt{5}$.
点评 本题考查的是三角形的外接圆与外心,掌握圆周角定理、灵活运用勾股定理是解题的关键.

练习册系列答案
相关题目
7.在-(-1),-|-3.14|,0,-(-3)5中,正数有( )个.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
12.下列关于 x的方程:①ax2+bx+c=0;②x2+$\frac{3}{x}$=6;③x2=0;④x=3x2⑤(x+1)(x-1)=x2+4x中,一元二次方程的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
2.已知△ABC的三边长a,b,c,化简|a+b-c|+|b-a-c|的结果是( )
| A. | 2a | B. | 2b | C. | 2a+2b | D. | 2b-2c |
 已知,如图A、B分别为数轴上的两点,A点对应的数为-10,B点对应的数为70
已知,如图A、B分别为数轴上的两点,A点对应的数为-10,B点对应的数为70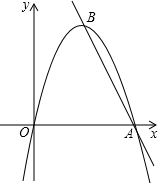 如图,抛物线y=ax2+bx与x轴的正半轴交于点A,抛物线的顶点为B,且点B的纵坐标为6,直线y=kx-6k经过A、B两点.
如图,抛物线y=ax2+bx与x轴的正半轴交于点A,抛物线的顶点为B,且点B的纵坐标为6,直线y=kx-6k经过A、B两点.