题目内容
已知二次函数y=ax2+2x+c的图象经过点A(1,0),并经过一次函数y=(2-k)x+k的图象与y轴的交点B,如果B到x轴的距离是3,求二次函数和一次函数的解析式.
考点:待定系数法求二次函数解析式,待定系数法求一次函数解析式
专题:计算题
分析:把A坐标代入二次函数解析式得到a与c的关系式,根据题意确定出B坐标,代入二次函数解析式,求出a与c的值,确定出二次函数解析式,将B坐标代入一次函数解析式求出k的值,即可确定出解析式.
解答:解:把A(1,0)代入二次函数解析式得:a+2+c=0,即a+c=-2,
由题意得:B坐标为(0,3)或(0,-3),
当B为(0,3)时,代入二次函数解析式得:c=3,此时a=-5,二次函数解析式为y=-5x2+2x+3,
把(0,3)代入一次函数解析式得:3=k,即一次函数解析式为y=-x+3;
当B为(0,-3)时,代入二次函数解析式得:c=-3,此时a=1,二次函数解析式为y=x2+2x-3,
把(0,-3)代入一次函数解析式得:k=-3,即一次函数解析式为y=5x-3.
由题意得:B坐标为(0,3)或(0,-3),
当B为(0,3)时,代入二次函数解析式得:c=3,此时a=-5,二次函数解析式为y=-5x2+2x+3,
把(0,3)代入一次函数解析式得:3=k,即一次函数解析式为y=-x+3;
当B为(0,-3)时,代入二次函数解析式得:c=-3,此时a=1,二次函数解析式为y=x2+2x-3,
把(0,-3)代入一次函数解析式得:k=-3,即一次函数解析式为y=5x-3.
点评:此题考查了待定系数法求二次函数解析式,待定系数法求一次函数解析式,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
反比例函数y=
(k为常数,k≠0)的自变量x的取值范围是( )
| k |
| x |
| A、x>0 | B、x≠0 |
| C、x≥0 | D、k≠0 |
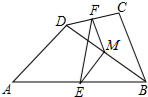 在四边形ABCD中,E、F、M分别是AB、CD、BD的中点,AD=BC.求证:∠EFM=∠FEM.
在四边形ABCD中,E、F、M分别是AB、CD、BD的中点,AD=BC.求证:∠EFM=∠FEM.