题目内容
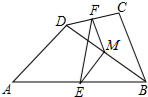 在四边形ABCD中,E、F、M分别是AB、CD、BD的中点,AD=BC.求证:∠EFM=∠FEM.
在四边形ABCD中,E、F、M分别是AB、CD、BD的中点,AD=BC.求证:∠EFM=∠FEM.考点:三角形中位线定理,等腰三角形的判定与性质
专题:证明题
分析:根据三角形的中位线平行于第三边并且等于第三边的一半可得ME=
AD,MF=
BC,然后求出ME=MF,再根据等边对等角证明即可.
| 1 |
| 2 |
| 1 |
| 2 |
解答:证明:∵E、F、M分别是AB、CD、BD的中点,
∴ME是△ABD的中位线,MF是△BCD的中位线,
∴ME=
AD,MF=
BC,
∵AD=BC,
∴ME=MF,
∴∠EFM=∠FEM.
∴ME是△ABD的中位线,MF是△BCD的中位线,
∴ME=
| 1 |
| 2 |
| 1 |
| 2 |
∵AD=BC,
∴ME=MF,
∴∠EFM=∠FEM.
点评:本题考查了三角形的中位线平行于第三边并且等于第三边的一半,等腰三角形的判定与性质,熟记定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 在Rt△ABC中,∠C=90°,AC=
在Rt△ABC中,∠C=90°,AC=