题目内容
15.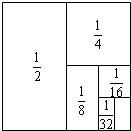 如图,把一个面积为1的正方形等分成两个面积为$\frac{1}{2}$的长方形,接着再把面积为$\frac{1}{2}$的一个长方形分成两个面积为$\frac{1}{4}$的长方形,再把面积为$\frac{1}{4}$的一个长方形分成两个面积为$\frac{1}{8}$的长方形,如此进行下去.
如图,把一个面积为1的正方形等分成两个面积为$\frac{1}{2}$的长方形,接着再把面积为$\frac{1}{2}$的一个长方形分成两个面积为$\frac{1}{4}$的长方形,再把面积为$\frac{1}{4}$的一个长方形分成两个面积为$\frac{1}{8}$的长方形,如此进行下去.(1)第8次等分所得的一个小长方形面积为多少?
(2)试利用图形揭示的规律计算:$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+$\frac{1}{16}$+$\frac{1}{32}$+$\frac{1}{64}$+$\frac{1}{128}$+$\frac{1}{256}$.
分析 (1)设第n次等分所得的一个小长方形面积为an(n为正整数),根据面积的变化找出变化规律“an=$(\frac{1}{2})^{n}$”,以此规律即可得出结论;
(2)结合图形可知$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+$\frac{1}{16}$+$\frac{1}{32}$+$\frac{1}{64}$+$\frac{1}{128}$+$\frac{1}{256}$=1-$\frac{1}{256}$,算出结论即可.
解答 解:(1)设第n次等分所得的一个小长方形面积为an(n为正整数),
观察,发现规律:a1=$\frac{1}{2}$,a2=$\frac{1}{4}$,a3=$\frac{1}{8}$,a4=$\frac{1}{16}$,…,
∴an=$(\frac{1}{2})^{n}$,
当n=8时,a8=$\frac{1}{256}$,
∴第8次等分所得的一个小长方形面积为$\frac{1}{256}$.
(2)根据图形可知:$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+$\frac{1}{16}$+$\frac{1}{32}$+$\frac{1}{64}$+$\frac{1}{128}$+$\frac{1}{256}$=1-$\frac{1}{256}$=$\frac{255}{256}$.
点评 本题考查了规律型中数字的变化类,根据面积的变化找出变化规律是解题的关键.

练习册系列答案
相关题目
5.下列从左到右的变形,其中是因式分解的是( )
| A. | 2(a-b)=2a-2b | B. | x2-2x+1=x(x-2)+1 | ||
| C. | (m+1)(m-1)=m2-1 | D. | 3a(a-1)+(1-a)=(3a-1)(a-1) |
3.已知a-2b=3,则3(a-b)-(a+b)的值为( )
| A. | 3 | B. | 6 | C. | -3 | D. | -6 |

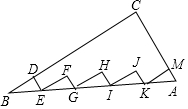 如图,在△ABC中,∠C=90°,AC=6,BC=8,点D、M分别在BC、AC上,Rt△BDE、Rt△EFG、Rt△GHI、Rt△IJK、Rt△KMA的斜边都在AB上,则五个小直角三角形的周长和为24.
如图,在△ABC中,∠C=90°,AC=6,BC=8,点D、M分别在BC、AC上,Rt△BDE、Rt△EFG、Rt△GHI、Rt△IJK、Rt△KMA的斜边都在AB上,则五个小直角三角形的周长和为24. 已知二次函数y=ax2+bx+c的图象如图,其对称轴x=-1,给出下列结果:①b2>4ac;②abc>0;③2a+b=0;④a-b+c<0;⑤3a+c>0.其中正确结论的序号是①④⑤.
已知二次函数y=ax2+bx+c的图象如图,其对称轴x=-1,给出下列结果:①b2>4ac;②abc>0;③2a+b=0;④a-b+c<0;⑤3a+c>0.其中正确结论的序号是①④⑤.