题目内容
15.若△ABC的三边a、b、c满足a2+b2+c2+338=10a+24b+26c,则△ABC的形状为( )| A. | 锐角三角形 | B. | 直角三角形 | C. | 等腰直角三角形 | D. | 钝角三角形 |
分析 先移项,把a2+b2+c2+338=10a+24b+26c变形成(a-[])2+(b-[])2+(c-[])2=0的形式,根据非负数的和为0,确定a、b、c的值,再根据a、b、c的值确定三角形的形状.
解答 解:∵a2+b2+c2+338=10a+24b+26c,
即a2+b2+c2+338-10a-24b-26c=0,
∴(a2-10a+25)+(b2-24b+144)+(c2-26c+169)=0,
∴(a-5)2+(b-12)2+(c-13)2=0
由于(a-5)2≥0,(b-12)2≥0,(c-13)2≥0
所以a-5=0,b-12=0,c-13=0,
即a=5,b=12,c=13.
因为52+122=132
所以△ABC是直角三角形.
故选B.
点评 本题考查了非负数的和为0、完全平方公式、勾股定理.变形题目给出等式为非负数的和确定a、b、c的值是关键.常见的非负数有:|a|、$\sqrt{a}$、a2.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
3.下列说法中正确的是( )
| A. | 正整数与正分数统称为正有理数 | B. | 正整数与负整数统称为整数 | ||
| C. | 正分数、0、负分数统称为分数 | D. | 一个有理数不是正数就是负数 |
 如图,AB为⊙O的切线,切点为B,连接AO,AO与⊙O交于点C,BD为⊙O的直径,连接CD,若∠A=30°,⊙O的半径为2,则图中阴影部分的面积为$\frac{4}{3}$π-$\sqrt{3}$(结果保留π)
如图,AB为⊙O的切线,切点为B,连接AO,AO与⊙O交于点C,BD为⊙O的直径,连接CD,若∠A=30°,⊙O的半径为2,则图中阴影部分的面积为$\frac{4}{3}$π-$\sqrt{3}$(结果保留π) 如图,一张长方形纸片ABCD沿EF折叠,若∠DEF=110°,∠DEA=40度.
如图,一张长方形纸片ABCD沿EF折叠,若∠DEF=110°,∠DEA=40度.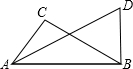 如图,已知∠ABD=∠C=90°,AD=12,AC=BD,∠BAD=30°,试求BC的长.
如图,已知∠ABD=∠C=90°,AD=12,AC=BD,∠BAD=30°,试求BC的长.