题目内容
如图①,矩形ABCD中,AB=4,O是CD上一点,且∠ABO=30°.
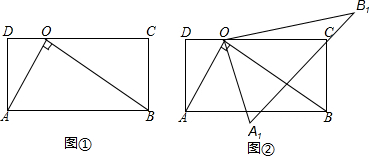
(1)直接写出OC的长;
(2)将△AOB沿OB边翻折得到△A′OB,且A'B交CD于M,请在图①中画出△A′OB,并求出OM的长;
(3)如图②,将△AOB绕点O逆时针旋转α角,得到△OA1B1,此时,A1B1恰好过顶点C,求sinα的值.

(1)直接写出OC的长;
(2)将△AOB沿OB边翻折得到△A′OB,且A'B交CD于M,请在图①中画出△A′OB,并求出OM的长;
(3)如图②,将△AOB绕点O逆时针旋转α角,得到△OA1B1,此时,A1B1恰好过顶点C,求sinα的值.
考点:矩形的性质,翻折变换(折叠问题),旋转的性质
专题:
分析:(1)求出∠DAO=∠ABO=30°,然后根据直角三角形30°角所对的直角边等于斜边的一半求出AO、DO,再根据矩形的对边相等求出CD,然后根据OC=CD-DO计算即可得解;
(2)根据翻折的性质可得OA=OA′,然后判断出OM是△A′AB的中位线,根据三角形的中位线平行于第三边并且等于第三边的一半可得OM=
AB;
(3)过点O作OP⊥A1B1于P,根据旋转的性质求出∠A1,OA1,再求出OP,然后求出∠3等于旋转角,再根据锐角三角函数的正弦等于对边比斜边列式即可.
(2)根据翻折的性质可得OA=OA′,然后判断出OM是△A′AB的中位线,根据三角形的中位线平行于第三边并且等于第三边的一半可得OM=
| 1 |
| 2 |
(3)过点O作OP⊥A1B1于P,根据旋转的性质求出∠A1,OA1,再求出OP,然后求出∠3等于旋转角,再根据锐角三角函数的正弦等于对边比斜边列式即可.
解答:解:(1)∵∠ABO+∠BAO=∠DAO+∠BAO=90°,
∴∠DAO=∠ABO=30°,
∴AO=
AB=
×4=2,
DO=
AO=
×2=1,
∵矩形ABCD中,AB=4,
∴CD=AB=4,
∴OC=CD-DO=4-1=3;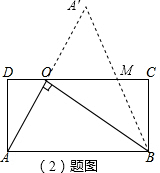
(2)如图,由翻折变换的性质得,OA=OA′,
∵OM∥AB,
∴OM是△A′AB的中位线,
∴OM=
AB=
×4=2;
(3)如图,过点O作OP⊥A1B1于P,
在Rt△OA1P中,∠A1=∠BAO=90°-30°=60°,OA1=OA=2,
∴A1P=
OA1=
×2=1,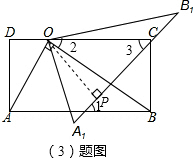
OP=
=
=
,
∵∠ABO+∠1=∠B1+∠2,∠ABO=∠B1,
∴∠1=∠2,
∵AB∥CD,
∴∠1=∠3,
∴∠3=∠1=∠α,
在Rt△OPC中,OC=3,
∴sinα=
=
.
∴∠DAO=∠ABO=30°,
∴AO=
| 1 |
| 2 |
| 1 |
| 2 |
DO=
| 1 |
| 2 |
| 1 |
| 2 |
∵矩形ABCD中,AB=4,
∴CD=AB=4,
∴OC=CD-DO=4-1=3;

(2)如图,由翻折变换的性质得,OA=OA′,
∵OM∥AB,
∴OM是△A′AB的中位线,
∴OM=
| 1 |
| 2 |
| 1 |
| 2 |
(3)如图,过点O作OP⊥A1B1于P,
在Rt△OA1P中,∠A1=∠BAO=90°-30°=60°,OA1=OA=2,
∴A1P=
| 1 |
| 2 |
| 1 |
| 2 |

OP=
| OA12-A1P2 |
| 22-12 |
| 3 |
∵∠ABO+∠1=∠B1+∠2,∠ABO=∠B1,
∴∠1=∠2,
∵AB∥CD,
∴∠1=∠3,
∴∠3=∠1=∠α,
在Rt△OPC中,OC=3,
∴sinα=
| OP |
| OC |
| ||
| 3 |
点评:本题考查了矩形的性质,翻折变换的性质,旋转的性质,锐角三角函数,直角三角形30°角所对的直角边等于斜边的一半以及三角形的中位线平行于第三边并且等于第三边的一半,熟记各性质并作辅助线是解题的关键.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
 已知如图直线AB∥CD,∠A=40°且AE=AF,则∠DCF=( )
已知如图直线AB∥CD,∠A=40°且AE=AF,则∠DCF=( )| A、110° | B、120° |
| C、130° | D、140° |
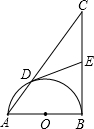 如图,已知直角△ABC中,∠ABC=90°,以AB为直径的⊙O与AC交于点D,点E在线段BC上且DE=BE.
如图,已知直角△ABC中,∠ABC=90°,以AB为直径的⊙O与AC交于点D,点E在线段BC上且DE=BE. 已知:如图,正方形ABCD,E,F分别为DC,BC中点.
已知:如图,正方形ABCD,E,F分别为DC,BC中点. 在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地,乙骑摩托车从B地到A地,到达A地后立即按原路返回,是甲、乙两人离B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题:
在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地,乙骑摩托车从B地到A地,到达A地后立即按原路返回,是甲、乙两人离B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题: