题目内容
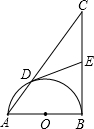 如图,已知直角△ABC中,∠ABC=90°,以AB为直径的⊙O与AC交于点D,点E在线段BC上且DE=BE.
如图,已知直角△ABC中,∠ABC=90°,以AB为直径的⊙O与AC交于点D,点E在线段BC上且DE=BE.(1)求证:DE是⊙O的切线;
(2)连结OE,若AC=6,求OE的长.
考点:切线的判定,三角形中位线定理
专题:
分析:(1)证明:连接0E,0D,根据BO=OD,DE=BE,OE=OE,可证明△DOE≌△BOE,即可得出∠ODE=∠ABC=90°,再由点D在圆上,即可得出DE是⊙O的切线;
(2)可证明OE是△ABC的中位线,可得出OE=3.
(2)可证明OE是△ABC的中位线,可得出OE=3.
解答: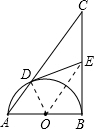 (1)证明:连接OE,OD,
(1)证明:连接OE,OD,
在△DOE和△BOE中,
,
∴△DOE≌△BOE,
∴∠ODE=∠ABC=90°°,
∵点D在圆上,
∴DE是⊙O的切线;
(2)解:∵DE是⊙O的切线,
∴OD⊥DE,
∴∠ODE=90°,
∴∠CDE+∠ADO=90°,
又∵∠A+∠C=90°,∠A=∠ODA,
∴∠C=∠CDE,
∴CE=DE,
∴点E为BC的中点,
∵O为AB的中点,
∴OE是△ABC的中位线,
∵AC=6,
∴OE=3.
 (1)证明:连接OE,OD,
(1)证明:连接OE,OD,在△DOE和△BOE中,
|
∴△DOE≌△BOE,
∴∠ODE=∠ABC=90°°,
∵点D在圆上,
∴DE是⊙O的切线;
(2)解:∵DE是⊙O的切线,
∴OD⊥DE,
∴∠ODE=90°,
∴∠CDE+∠ADO=90°,
又∵∠A+∠C=90°,∠A=∠ODA,
∴∠C=∠CDE,
∴CE=DE,
∴点E为BC的中点,
∵O为AB的中点,
∴OE是△ABC的中位线,
∵AC=6,
∴OE=3.
点评:本题考查了切线的判定和性质以及三角形的中位线定理,要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
相关题目
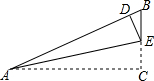 小明在学习“锐角三角函数”中发现,将如图的含30°(∠BAC)角的直角三角形纸片ABC沿过点A的直线折叠,使点C落在AB上的点D处,这样就可以求出75°角的正切值是( )
小明在学习“锐角三角函数”中发现,将如图的含30°(∠BAC)角的直角三角形纸片ABC沿过点A的直线折叠,使点C落在AB上的点D处,这样就可以求出75°角的正切值是( )




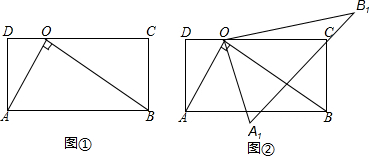
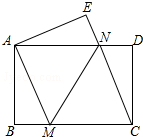 如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直线MN交BC于点M,交AD于点N.
如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直线MN交BC于点M,交AD于点N.