题目内容
4. 如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,求AC长.
如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,求AC长.
分析 过D作DF⊥AC于F,根据角平分线性质求出DF=DE=2,根据S△ADB+S△ADC=7和三角形面积公式求出即可.
解答 解:
过D作DF⊥AC于F,
∵AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,DE=2,
∴DE=DF=2,
∵S△ABC=7,
∴S△ADB+S△ADC=7,
∴$\frac{1}{2}×AB×DE+\frac{1}{2}×AC×DF$=7,
∴$\frac{1}{2}×4×2+\frac{1}{2}×AC×2$=7,
解得:AC=3.
点评 本题考查了角的平分线性质,三角形面积公式的应用,能正确作出辅助线是解此题的关键,注意:角平分线上的点到角两边的距离相等.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
12. 如图,∠AOB是直角,∠AOC=38°,OD平分∠BOC,则∠AOD的度数为( )
如图,∠AOB是直角,∠AOC=38°,OD平分∠BOC,则∠AOD的度数为( )
 如图,∠AOB是直角,∠AOC=38°,OD平分∠BOC,则∠AOD的度数为( )
如图,∠AOB是直角,∠AOC=38°,OD平分∠BOC,则∠AOD的度数为( )| A. | 52° | B. | 38° | C. | 64° | D. | 26° |
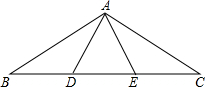 如图,已知点D,E是BC上的三等分点,△ADE是等边三角形,那么∠BAC的度数为120°.
如图,已知点D,E是BC上的三等分点,△ADE是等边三角形,那么∠BAC的度数为120°. 尺规作图(不写作法,保留作图痕迹)
尺规作图(不写作法,保留作图痕迹) 在Rt△AOD中,∠AOD=90°,点B、C在OD上,且OA=OB=BC=CD,求证:∠1+∠2+∠3=90°.
在Rt△AOD中,∠AOD=90°,点B、C在OD上,且OA=OB=BC=CD,求证:∠1+∠2+∠3=90°.