题目内容
14. 在Rt△AOD中,∠AOD=90°,点B、C在OD上,且OA=OB=BC=CD,求证:∠1+∠2+∠3=90°.
在Rt△AOD中,∠AOD=90°,点B、C在OD上,且OA=OB=BC=CD,求证:∠1+∠2+∠3=90°.
分析 由已知条件∠AOD=90°,设OA=OB=BC=CD=x,根据勾股定理得到AB=$\sqrt{2}$x,AC=$\sqrt{5}$x,AD=$\sqrt{10}$x,OC=2x,OD=3x,BD=2x,证得$\frac{AB}{BD}$=$\frac{BC}{AB}$=$\frac{AC}{DA}$,得到△ABC∽△DBA,根据相似三角形的性质得到∠3=∠BAC,由三角形的外角的性质得到∠1=∠BAC+∠2=45°,即可得到结论.
解答 证明:∵∠AOD=90°,设OA=OB=BC=CD=x
∴AB=$\sqrt{2}$x,AC=$\sqrt{5}$x,AD=$\sqrt{10}$x,OC=2x,OD=3x,BD=2x
∴$\frac{AB}{BD}$=$\frac{\sqrt{2}x}{2x}$=$\frac{\sqrt{2}}{2}$,$\frac{BC}{AB}$=$\frac{x}{\sqrt{2}x}$=$\frac{\sqrt{2}}{2}$,$\frac{AC}{DA}$=$\frac{\sqrt{5}x}{\sqrt{10}x}$=$\frac{\sqrt{2}}{2}$,
∴$\frac{AB}{BD}$=$\frac{BC}{AB}$=$\frac{AC}{DA}$,
∴△ABC∽△DBA,
∴∠3=∠BAC,
∵∠1=∠BAC+∠2=45°,
∴∠3+∠2=45°,
∴∠1+∠2+∠3=90°.
点评 此题考查了相似三角形的判定和性质,等腰直角三角形的性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
2.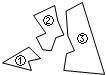 某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么可行的办法是( )
某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么可行的办法是( )
 某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么可行的办法是( )
某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么可行的办法是( )| A. | 带①③去 | B. | 带①去 | C. | 带②去 | D. | 带③去 |
 如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,求AC长.
如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,求AC长.