题目内容
20.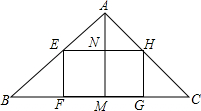 在△ABC中,己知BC=20cm,BC边上的高AM=16cm,在三角形内截取一个面积最大的矩形,并使它的一边在BC上,求此时矩形的长和宽.
在△ABC中,己知BC=20cm,BC边上的高AM=16cm,在三角形内截取一个面积最大的矩形,并使它的一边在BC上,求此时矩形的长和宽.
分析 设矩形EFGH的宽EF=x,根据相似三角形对应高的比等于相似比列式求出EH,再根据矩形的面积列式整理,然后根据二次函数的最值问题解答即可
解答 解:如图,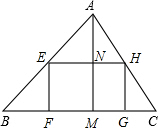 设矩形EFGH的宽EF=x,则AN=AM-MN=12-x,
设矩形EFGH的宽EF=x,则AN=AM-MN=12-x,
∵矩形的对边EH∥FG,
∴△AEH∽△ABC,
∴$\frac{AN}{AM}=\frac{EH}{BC}$,
即$\frac{16-x}{16}=\frac{EH}{20}$,
解得:EH=20-$\frac{5x}{4}$,
四边形EFGH的面积=x•(20-$\frac{5x}{4}$)=-$\frac{5}{4}$x2+20x=-$\frac{5}{4}$(x-8)2+80,
所以,当x=8,即EF=8时,四边形EFGH最大面积为80cm2,
此时EH=20-$\frac{5}{4}×8$=10,
∴此时矩形的长和宽分别是10cm,8cm.
点评 本题考查了相似三角形的应用,二次函数的最值问题,根据相似三角形的对应高的比等于相似比用矩形EFGH的宽表示出长是解题的关键.

练习册系列答案
相关题目
15.一段斜坡公路的坡度为i=1:2$\sqrt{2}$,这段公路长为150m,则从坡底到坡顶这段公路升高( )
| A. | 75m | B. | 50m | C. | 75$\sqrt{2}$m | D. | 50$\sqrt{2}$m |
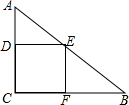 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点E在AB上,点D在AC上,若矩形DEFC的面积为12,则这个矩形的长和宽分别是多少?
如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点E在AB上,点D在AC上,若矩形DEFC的面积为12,则这个矩形的长和宽分别是多少? 如图,正方形ABCD的边长为4,P是BC边上一点,QP⊥AP交DC于Q,如果BP=x,△ADQ的面积为y,用含x的代数式表示y.
如图,正方形ABCD的边长为4,P是BC边上一点,QP⊥AP交DC于Q,如果BP=x,△ADQ的面积为y,用含x的代数式表示y.