题目内容
15．已知2sin2α-3$\sqrt{3}$sinα+3=0中，α为锐角，则sinα=$\frac{\sqrt{3}}{2}$．分析 根据公式法解方程解方程，可得sinα．
解答 解：2sin2α-3$\sqrt{3}$sinα+3=0，a=2，b=-3$\sqrt{3}$，c=3．
△=b2-4ac=（-3$\sqrt{3}$）2-4×2×3=3＞0，
sinα=$\frac{3\sqrt{3}±\sqrt{3}}{4}$，sinα=$\sqrt{3}$（不符合题意的解要舍去），sinα=$\frac{\sqrt{3}}{2}$，
故答案为：$\frac{\sqrt{3}}{2}$．
点评 本题考查了解方程，利用公式法解方程，注意确定a、b、c的值是解题关键．
练习册系列答案
相关题目
20．某生活小区鲜奶店每天以每瓶3元的价格从奶场购进优质鲜奶，然后以每瓶5元的价格出售，如果当天卖不完，剩余的只有倒掉．店主记录了30天的日需求量（单位：瓶），整理得下表：
（1）求这30天内日需求量的众数和中位数；
（2）如果一年按365天计算，试估计一年中鲜奶店的总利润（单位：元）．
| 日需求量 | 26 | 27 | 28 | 29 | 31 |
| 天数 | 5 | 8 | 7 | 6 | 4 |
（2）如果一年按365天计算，试估计一年中鲜奶店的总利润（单位：元）．
如图，已知⊙O是△ABC的内切圆，切点为D、E、F，如果AE=1，CD=2，BF=3，且△ABC的面积为6，求内切圆的半径r．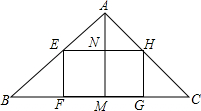
在△ABC中，己知BC=20cm，BC边上的高AM=16cm，在三角形内截取一个面积最大的矩形，并使它的一边在BC上，求此时矩形的长和宽．
如图，△ABC在平面直角坐标系中第二象限内，顶点A的坐标是（-2，3），先把△ABC向右平移4个单位得到△A1B1C1，再作△A1B1C1关于x轴对称图形△A2B2C2，则顶点A2的坐标是（2，-3）．