题目内容
5.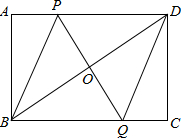 如图,矩形ABCD中,点P是线段AD上一动点,O为BD的中点,PO的延长线交BC于Q.
如图,矩形ABCD中,点P是线段AD上一动点,O为BD的中点,PO的延长线交BC于Q.(1)求证:OP=OQ;
(2)若AD=4厘米,AB=3厘米,当AP为何值时,四边形PBQD是菱形,并加以说明.
分析 (1)根据矩形性质推出AD∥BC,根据平行线的性质得出∠PDO=∠QBO,根据全等三角形的判定ASA证△PDO≌△BQO,根据全等三角形的性质推出即可.
(2)由菱形的性质得出BP=PD,设AP=x厘米,则BP=PD=(4-x)厘米,由勾股定理得出方程,解方程即可.
解答 (1)证明:∵四边形ABCD是矩形,
∴AD∥BC,∠A=90°,
∴∠PDO=∠QBO,
∵O为BD中点,
∴OB=OD,
在△PDO和△QBO中,
$\left\{\begin{array}{l}{∠PDO=∠QBO}&{\;}\\{OB=OD}&{\;}\\{∠POD=∠BOQ}&{\;}\end{array}\right.$,
∴△PDO≌△BQO(ASA),
∴OP=OQ.
(2)解:当AP=$\frac{7}{8}$时,四边形PBQD是菱形;理由如下:
∵OB=OD,OP=OQ,
∴四边形PBQD是平行四边形,
当四边形PBQD是菱形时,BP=PD,
设AP=x厘米,则BP=PD=(4-x)厘米,
由勾股定理得:X2+32=(4-x)2,
解得:x=$\frac{7}{8}$,
即当AP为$\frac{7}{8}$厘米时,四边形PBQD是菱形.
点评 本题考查了矩形的性质,全等三角形的性质和判定,平行四边形的判定,菱形的判定与性质;题目比较好,综合性比较强.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15. 函数y=x2+2x-3的图象如图所示,当x=m时,y<0,则m的值可能是( )
函数y=x2+2x-3的图象如图所示,当x=m时,y<0,则m的值可能是( )
 函数y=x2+2x-3的图象如图所示,当x=m时,y<0,则m的值可能是( )
函数y=x2+2x-3的图象如图所示,当x=m时,y<0,则m的值可能是( )| A. | -4 | B. | $\frac{1}{2}$ | C. | 2 | D. | 3 |
10.若方程x|a|-2-7=0是一个一元一次方程,则a等于( )
| A. | -3 | B. | 3 | C. | ±3 | D. | 0 |
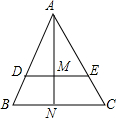 如图,已知△ABC中,DE∥BC,DE=8,BC=12,AN⊥BC交DE于M,四边形BCED的面积为90.求△ADE的面积及AM、AN的长.
如图,已知△ABC中,DE∥BC,DE=8,BC=12,AN⊥BC交DE于M,四边形BCED的面积为90.求△ADE的面积及AM、AN的长.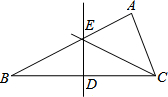 如图,在Rt△ABC中,∠A=90°,BC边的垂直平分线交BC于点D,交AB与E,若CE平分∠ACB,EC=5,ED=3,则AB的长是8.
如图,在Rt△ABC中,∠A=90°,BC边的垂直平分线交BC于点D,交AB与E,若CE平分∠ACB,EC=5,ED=3,则AB的长是8.