题目内容
15. 函数y=x2+2x-3的图象如图所示,当x=m时,y<0,则m的值可能是( )
函数y=x2+2x-3的图象如图所示,当x=m时,y<0,则m的值可能是( )| A. | -4 | B. | $\frac{1}{2}$ | C. | 2 | D. | 3 |
分析 先求出抛物线与x轴的交点坐标,利用函数图象即可得出结论.
解答 解:∵函数y=x2+2x-3=(x-1)(x+3),
∴函数图象与x轴的交点为(1,0),(-3,0).
∵当x=m时,y<0,
∴-3<m<1.
故选B.
点评 本题考查的是二次函数与不等式,能根据题意画出图形,利用数形结合求解是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.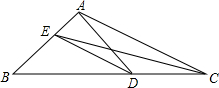 如图,在△ABC中,点D是BC上的一点,已知∠DAC=30°,∠DAB=75°,CE平分∠ACB交AB于点E,连接DE,则∠DEC=( )
如图,在△ABC中,点D是BC上的一点,已知∠DAC=30°,∠DAB=75°,CE平分∠ACB交AB于点E,连接DE,则∠DEC=( )
 如图,在△ABC中,点D是BC上的一点,已知∠DAC=30°,∠DAB=75°,CE平分∠ACB交AB于点E,连接DE,则∠DEC=( )
如图,在△ABC中,点D是BC上的一点,已知∠DAC=30°,∠DAB=75°,CE平分∠ACB交AB于点E,连接DE,则∠DEC=( )| A. | 10° | B. | 15° | C. | 20° | D. | 25° |
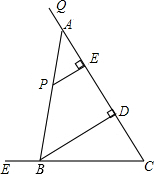 如图,tan∠QCF=2,点E在射线CQ上,CE=12,点P是∠QCF内一点,PE⊥QC于点E,PE=4,在射线CQ上取一点A,连AP并延长射线CF于点B,作BD⊥QC于点D.
如图,tan∠QCF=2,点E在射线CQ上,CE=12,点P是∠QCF内一点,PE⊥QC于点E,PE=4,在射线CQ上取一点A,连AP并延长射线CF于点B,作BD⊥QC于点D.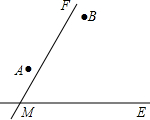 两个城镇A、B与两条公路ME,MF位置如图所示,其中ME是东西方向的公路.现电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A、B的距离必须相等,到两条公路ME,MF的距离也必须相等,且在∠FME的内部.
两个城镇A、B与两条公路ME,MF位置如图所示,其中ME是东西方向的公路.现电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A、B的距离必须相等,到两条公路ME,MF的距离也必须相等,且在∠FME的内部.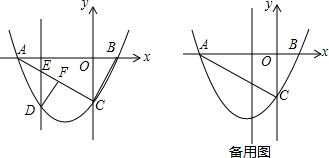
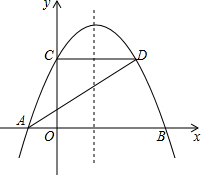 如图,已知抛物线y=ax2+$\frac{4}{3}$x+c与x轴交于A、B两点,与y轴交于点C,点D在抛物线上,且A(-1,0),D(2,2).
如图,已知抛物线y=ax2+$\frac{4}{3}$x+c与x轴交于A、B两点,与y轴交于点C,点D在抛物线上,且A(-1,0),D(2,2).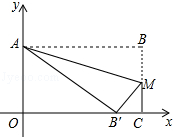 矩形OABC在平面直角坐标系中的位置如图所示,O为坐标原点,OA与y轴重合,OC与x轴重合,M为BC上点,沿AM折叠矩形使得点B′落在OC上,且知
矩形OABC在平面直角坐标系中的位置如图所示,O为坐标原点,OA与y轴重合,OC与x轴重合,M为BC上点,沿AM折叠矩形使得点B′落在OC上,且知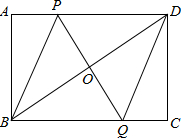 如图,矩形ABCD中,点P是线段AD上一动点,O为BD的中点,PO的延长线交BC于Q.
如图,矩形ABCD中,点P是线段AD上一动点,O为BD的中点,PO的延长线交BC于Q.