题目内容
13.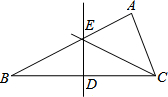 如图,在Rt△ABC中,∠A=90°,BC边的垂直平分线交BC于点D,交AB与E,若CE平分∠ACB,EC=5,ED=3,则AB的长是8.
如图,在Rt△ABC中,∠A=90°,BC边的垂直平分线交BC于点D,交AB与E,若CE平分∠ACB,EC=5,ED=3,则AB的长是8.
分析 由BC边的垂直平分线交BC于点D,得出BE=EC,由CE平分∠ACB得出,得出AE=DE,进一步求得AB即可.
解答 解:∵DE是BC边的垂直平分线,
∴BE=EC=5,ED⊥BC,
∵CE平分∠ACB,EA⊥AC,
∴EA=ED=3,
∴AB=AE+EB=ED+EC=5+3=8.
故答案为:8.
点评 本题考查的是线段的垂直平分线的性质和角平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等,角平分线上的点到角的两边的距离相等是解题的关键.

练习册系列答案
相关题目
3.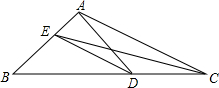 如图,在△ABC中,点D是BC上的一点,已知∠DAC=30°,∠DAB=75°,CE平分∠ACB交AB于点E,连接DE,则∠DEC=( )
如图,在△ABC中,点D是BC上的一点,已知∠DAC=30°,∠DAB=75°,CE平分∠ACB交AB于点E,连接DE,则∠DEC=( )
 如图,在△ABC中,点D是BC上的一点,已知∠DAC=30°,∠DAB=75°,CE平分∠ACB交AB于点E,连接DE,则∠DEC=( )
如图,在△ABC中,点D是BC上的一点,已知∠DAC=30°,∠DAB=75°,CE平分∠ACB交AB于点E,连接DE,则∠DEC=( )| A. | 10° | B. | 15° | C. | 20° | D. | 25° |
8.已知等腰△ABC的两边长分别为2和4,则等腰△ABC的周长为( )
| A. | 8 | B. | 10 | C. | 8或10 | D. | 12 |
18.下列图形中,是中心对称图形,而不是轴对称图形的是( )
| A. | 菱形 | B. | 平行四边形 | C. | 正六边形 | D. | 矩形 |
5.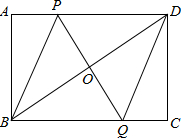 如图,矩形ABCD中,点P是线段AD上一动点,O为BD的中点,PO的延长线交BC于Q.
如图,矩形ABCD中,点P是线段AD上一动点,O为BD的中点,PO的延长线交BC于Q.
(1)求证:OP=OQ;
(2)若AD=4厘米,AB=3厘米,当AP为何值时,四边形PBQD是菱形,并加以说明.
 如图,矩形ABCD中,点P是线段AD上一动点,O为BD的中点,PO的延长线交BC于Q.
如图,矩形ABCD中,点P是线段AD上一动点,O为BD的中点,PO的延长线交BC于Q.(1)求证:OP=OQ;
(2)若AD=4厘米,AB=3厘米,当AP为何值时,四边形PBQD是菱形,并加以说明.
3. 某市对参加今年中考的50000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.请根据图表信息回答下列问题:
某市对参加今年中考的50000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.请根据图表信息回答下列问题:
(1)在频数分布表中,a的值为60,b的值为0.05,并将频数分布直方图补充完整;
(2)甲同学说“我的视力情况是此抽样调查所得数据的中位数”,问甲同学的视力情况应在什么范围内?
(3)若视力在4.9以上(含4.9)均属正常,则视力正常的人数占被统计人数的百分比是35%,并根据上述信息估计全市初中毕业生中视力正常的学生有多少人?
 某市对参加今年中考的50000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.请根据图表信息回答下列问题:
某市对参加今年中考的50000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.请根据图表信息回答下列问题:| 视力 | 频数(人) | 频率 |
| 4.0≤x<4.3 | 20 | 0.1 |
| 4.3≤x<4.6 | 40 | 0.2 |
| 4.6≤x<4.9 | 70 | 0.35 |
| 4.9≤x<5.2 | a | 0.3 |
| 5.2≤x<5.5 | 10 | b |
(2)甲同学说“我的视力情况是此抽样调查所得数据的中位数”,问甲同学的视力情况应在什么范围内?
(3)若视力在4.9以上(含4.9)均属正常,则视力正常的人数占被统计人数的百分比是35%,并根据上述信息估计全市初中毕业生中视力正常的学生有多少人?
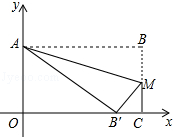 矩形OABC在平面直角坐标系中的位置如图所示,O为坐标原点,OA与y轴重合,OC与x轴重合,M为BC上点,沿AM折叠矩形使得点B′落在OC上,且知
矩形OABC在平面直角坐标系中的位置如图所示,O为坐标原点,OA与y轴重合,OC与x轴重合,M为BC上点,沿AM折叠矩形使得点B′落在OC上,且知