题目内容
2. 如图,点E在CA延长线上,DE、AB交于F,且∠BDE=∠AEF,∠B=∠C,∠EFA比∠FDC的余角小10°,P为线段DC上一动点,Q为PC上一点,且满足∠FQP=∠QFP,FM为∠EFP的平分线.则下列结论:
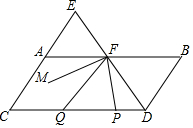
如图,点E在CA延长线上,DE、AB交于F,且∠BDE=∠AEF,∠B=∠C,∠EFA比∠FDC的余角小10°,P为线段DC上一动点,Q为PC上一点,且满足∠FQP=∠QFP,FM为∠EFP的平分线.则下列结论:①AB∥CD;
②FQ平分∠AFP;
③∠B+∠E=140°;
④∠QFM的角度为定值.
其中正确结论的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 ①由∠BDE=∠AEF可得出AE∥BD,进而可得出∠B=∠EAF,结合∠B=∠C可得出∠EAF=∠C,根据“同位角相等,两直线平行”可得出AB∥CD,结论①正确;②由AB∥CD可得出∠AFQ=∠FQP,结合∠FQP=∠QFP可得出∠AFQ=∠QFP,即FQ平分∠AFP,结论②正确;③由AB∥CD可得出∠EFA=∠FDC,结合∠EFA比∠FDC的余角小10°可求出∠EFA的度数,再由∠B=∠EAF结合三角形内角和定理可求出∠B+∠E=140°,结论③正确;④根据角平分线的定义可得出∠MFP=$\frac{1}{2}$∠EFA+$\frac{1}{2}$∠AFP以及∠QFP=$\frac{1}{2}$∠AFP,将其代入∠QFM=∠MFP-∠QFP可求出∠QFM的角度为定值20°,结论④正确.综上即可得出结论.
解答 解:①∵∠BDE=∠AEF,
∴∴AE∥BD,
∴∠B=∠EAF.
∵∠B=∠C,
∴∠EAF=∠C,
∴AB∥CD,结论①正确;
②∵AB∥CD,
∴∠AFQ=∠FQP.
∵∠FQP=∠QFP,
∴∠AFQ=∠QFP,
∴FQ平分∠AFP,结论②正确;
③∵AB∥CD,
∴∠EFA=∠FDC.
∵∠EFA比∠FDC的余角小10°,
∴∠EFA=40°.
∵∠B=∠EAF,∠EAF+∠E+∠EFA=180°,
∴∠B+∠E=180°-∠EFA=140°,结论③正确;
④∵FM为∠EFP的平分线,
∴∠MFP=$\frac{1}{2}$∠EFP=$\frac{1}{2}$∠EFA+$\frac{1}{2}$∠AFP.
∵∠AFQ=∠QFP,
∴∠QFP=$\frac{1}{2}$∠AFP,
∴∠QFM=∠MFP-∠QFP=$\frac{1}{2}$∠EFA=20°,结论④正确.
综上所述:正确的结论有①②③④.
故选D.
点评 本题考查了平行线的判定与性质、余角和补角、角平分线的定义以及三角形内角和定理,逐一分析四条结论的正误是解题的关键.

| A. | 2x+3y=5xy | B. | x2•x3=x6 | C. | (a3)2=a6 | D. | 4x6÷2x2=2x3 |
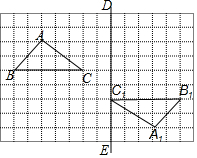 如图,在方格纸中,每个小正方形的边长都为1个单位长度,△ABC与△A1B1C1呈中心对称.
如图,在方格纸中,每个小正方形的边长都为1个单位长度,△ABC与△A1B1C1呈中心对称.