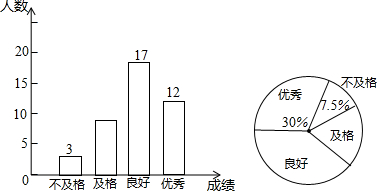
题目内容
12．已知（x+$\frac{1}{2}$）2+|y+3|=0，先化简再求值：3（x2-2xy）-[3x2-2y+2（xy+y）]．分析 原式去括号合并得到最简结果，利用非负数的性质求出x与y的值，代入计算即可求出值．
解答 解：原式=3x2-6xy-[3x2-2y+2xy+2y]
=3x2-6xy-（3x2+2xy）
=3x2-6xy-3x2-2xy
=-8xy，
由（x+$\frac{1}{2}$）2+|y+3|=0得：x=-$\frac{1}{2}$，y=-3，
将x=-$\frac{1}{2}$，y=-3 代入得：原式=-12．
点评 此题考查了整式的加减-化简求值，以及非负数的性质，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
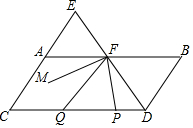如图，点E在CA延长线上，DE、AB交于F，且∠BDE=∠AEF，∠B=∠C，∠EFA比∠FDC的余角小10°，P为线段DC上一动点，Q为PC上一点，且满足∠FQP=∠QFP，FM为∠EFP的平分线．则下列结论：
17．
如图，图中x的值为（ ）
如图，图中x的值为（ ）| A． | 50° | B． | 60° | C． | 70° | D． | 75° |