题目内容
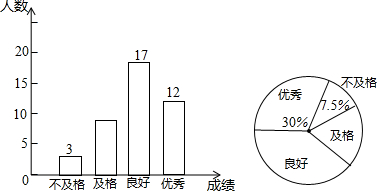
11.某农庄计划在30亩空地上全部种植蔬菜和水果,菜农小张和果农小李分别承包了种植蔬菜和水果的任务,小张种植每亩蔬菜的工资y(元)与种植面积m(亩)之间的函数关系如图1所示,小李种植水果所得报酬z(元)与种植面积n(亩)之间函数关系如图2所示.(1)如果种植蔬菜20亩,直接写出小张种植每亩蔬菜的工资是140元,小张应得的工资总额是2800元,此时,小李应得的报酬是1500元;
(2)当0≤n≤30时,求z与n之间的函数关系式;
(3)设农庄支付给小张和小李的总费用为w(元),当10<m≤30时,求w与m之间的函数关系式,并求出总费用最大为多少元.

分析 (1)根据图象数据解答即可;
(2)当0≤n≤30时,则与n之间的函数关系式分别为正比例函数(0≤n≤10)和一次函数(10<n≤30)然后利用待定系数法求函数解析式即可;
(3)先求出20<m≤30时y与m的函数关系式,再分①10<m≤20时,10<n≤20;②20<m≤30时,0<n≤10两种情况,根据总费用等于两人的费用之和列式整理即可得解.
解答 解:(1)由图可知,如果种植蔬菜20亩,则小张种植每亩蔬菜的工资是$\frac{1}{2}$(160+120)=140元,
小张应得的工资总额是:140×20=2800元,
此时,小李种植水果:30-20=10亩,
小李应得的报酬是1500元;
故答案为:140;2800;1500;
(2)当0≤n≤10时,设z=k′n,
∴函数图象经过点(10,1500),
∴k′=150,
∴z=150n;
当10<n≤30时,设z=kn+b(k≠0),
∵函数图象经过点(10,1500),(30,3900),
∴$\left\{\begin{array}{l}{10k+b=1500}\\{30k+b=3900}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=120}\\{b=300}\end{array}\right.$,
所以,z=120n+300(10<n≤30);
(3)当10<m≤30时,设y=km+b,
∵函数图象经过点(10,160),(30,120),
∴$\left\{\begin{array}{l}{10k+b=160}\\{30k+b=120}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-2}\\{b=180}\end{array}\right.$,
∴y=-2m+180,
∵m+n=30,
∴n=30-m,
∴①当10<m≤20时,10≤n<20,
w=m(-2m+180)+120n+300,
=m(-2m+180)+120(30-m)+300,
=-2m2+60m+3900,
②当20<m≤30时,0≤n<10,
w=m(-2m+180)+150n,
=m(-2m+180)+150(30-m),
=-2m2+30m+4500,
所以,w与m之间的函数关系式为w=$\left\{\begin{array}{l}{-2{m}^{2}+60m+3900(10<m≤20)}\\{-2{m}^{2}+30m+4500(20<m≤30)}\end{array}\right.$.
点评 本题考查了一次函数的应用,主要利用了待定系数法求一次函数解析式,(3)难点在于要分情况讨论并注意m、n的取值范围的对应关系,这也是本题最容易出错的地方.

 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案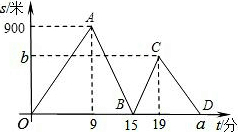 张强、刘明两位同学从实验中学出发到某中学参加作文比赛,张强不行行走一段时间后,刘明骑自行车沿同一条路线追赶,两人都是匀速前进,他们相距的路程s(单位:m)与张强出发的时间t(单位:min)之间的函数关系如图所示.
张强、刘明两位同学从实验中学出发到某中学参加作文比赛,张强不行行走一段时间后,刘明骑自行车沿同一条路线追赶,两人都是匀速前进,他们相距的路程s(单位:m)与张强出发的时间t(单位:min)之间的函数关系如图所示.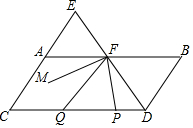 如图,点E在CA延长线上,DE、AB交于F,且∠BDE=∠AEF,∠B=∠C,∠EFA比∠FDC的余角小10°,P为线段DC上一动点,Q为PC上一点,且满足∠FQP=∠QFP,FM为∠EFP的平分线.则下列结论:
如图,点E在CA延长线上,DE、AB交于F,且∠BDE=∠AEF,∠B=∠C,∠EFA比∠FDC的余角小10°,P为线段DC上一动点,Q为PC上一点,且满足∠FQP=∠QFP,FM为∠EFP的平分线.则下列结论: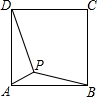 如图,点P是正方形ABCD内一点,PA=1,PD=$\sqrt{10}$,∠APB=135°,则PB的长为2$\sqrt{2}$.
如图,点P是正方形ABCD内一点,PA=1,PD=$\sqrt{10}$,∠APB=135°,则PB的长为2$\sqrt{2}$.