题目内容
17.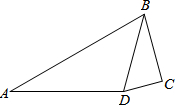 如图,在四边形ABCD中,∠A=30°,∠C=90°,∠ADB=105°,sin∠BDC=$\frac{{\sqrt{3}}}{2}$,AD=4.则DC的长=$\sqrt{2}$.
如图,在四边形ABCD中,∠A=30°,∠C=90°,∠ADB=105°,sin∠BDC=$\frac{{\sqrt{3}}}{2}$,AD=4.则DC的长=$\sqrt{2}$.
分析 作DH⊥AB于H,如图,在Rt△ADH中,由∠A=30°得到∠ADB=60°,DH=$\frac{1}{2}$AD=2,则可计算出∠BDH=45°,于是得到BD=$\sqrt{2}$DH=2$\sqrt{2}$,然后在Rt△BCD中,利用∠BDC的正弦可计算出BC=$\sqrt{6}$,再根据勾股定理可计算出CD的长.
解答 解:作DH⊥AB于H,如图, ∵∠A=30°,
∵∠A=30°,
∴∠ADB=60°,DH=$\frac{1}{2}$AD=2,
∵∠ADB=105°,
∴∠BDH=45°,
∴△BDH为等腰直角三角形,
∴BD=$\sqrt{2}$DH=2$\sqrt{2}$,
在Rt△BCD中,∵sin∠BDC=$\frac{BC}{BD}$=$\frac{\sqrt{3}}{2}$,
∴BC=2$\sqrt{2}$×$\frac{\sqrt{3}}{2}$=$\sqrt{6}$,
∴CD=$\sqrt{B{D}^{2}-B{C}^{2}}$=$\sqrt{2}$.
故答案为$\sqrt{2}$.
点评 本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.合理作辅助线构建特殊直角三角形是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.南京青奥会的成功举办,赢得了国际奥委会的高度赞扬,也促使了中国与世界各国青年的交流与沟通,据不完全统计,在青奥会举办期间,共有来自世界各地的约33.8万青年人相聚南京,33.8万用科学记数法表示为( )
| A. | 33.8×104 | B. | 3.38×104 | C. | 3.38×105 | D. | 0.338×106 |




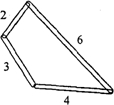 如图,用四个螺丝将四条不可弯曲的木条围成一个木框,不计螺丝大小,其中相邻两螺丝的距离依次为2、3、4、6,且相邻两木条的夹角均可调整.若调整木条的夹角时不破坏此木框,则任意两个螺丝间的距离的最大值为( )
如图,用四个螺丝将四条不可弯曲的木条围成一个木框,不计螺丝大小,其中相邻两螺丝的距离依次为2、3、4、6,且相邻两木条的夹角均可调整.若调整木条的夹角时不破坏此木框,则任意两个螺丝间的距离的最大值为( )