题目内容
2.在平面直角坐标系中,将二次函数y=ax2+bx+4的图象向左平移4个单位或向右平移1个单位都会经过原点,则该二次函数图象的顶点坐标为($\frac{3}{2}$,$\frac{25}{4}$).分析 根据题意得到该函数图象经过点(4,0)和(-1,0),将其分别代入函数解析式可以求得a、b的值.然后利用配方法将二次函数解析式转化为顶点式,据此可以得到该函数图象的顶点坐标.
解答 解:由题意知该函数图象经过点(4,0)和(-1,0),
则$\left\{\begin{array}{l}{16a+4b+4=0}\\{a-b+4=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-1}\\{b=3}\end{array}\right.$,
所以该函数解析式为y=-x2+3x+4=-(x-$\frac{3}{2}$)2+$\frac{25}{4}$.
故该函数顶点坐标是($\frac{3}{2}$,$\frac{25}{4}$).
故答案是:($\frac{3}{2}$,$\frac{25}{4}$).
点评 本题考查了二次函数图象与几何变换,二次函数图象上点的坐标特征.根据题意得到该抛物线经过点(4,0)和(-1,0)是解题的难点.

练习册系列答案
相关题目
10.一只不透明的袋子中装有1个白球,2个黄球和3个红球,每个球除颜色外都相同,将球搅匀,从中任意摸出一个球.如果想使摸到这三种颜色的球的概率相等,下列做法正确的是( )
| A. | 向袋子里分别投放1个白球,1个黄球,1个红球 | |
| B. | 向袋子里分别投放3个白球,2个黄球,1个红球 | |
| C. | 向袋子里分别投放2个白球,1个红球 | |
| D. | 向袋子里投放2个白球 |
11. 如图是函数y=$\frac{a}{x}$-1的图象,则关于x的分式方程$\frac{a}{x}$=3的解是( )
如图是函数y=$\frac{a}{x}$-1的图象,则关于x的分式方程$\frac{a}{x}$=3的解是( )
 如图是函数y=$\frac{a}{x}$-1的图象,则关于x的分式方程$\frac{a}{x}$=3的解是( )
如图是函数y=$\frac{a}{x}$-1的图象,则关于x的分式方程$\frac{a}{x}$=3的解是( )| A. | x=6 | B. | x=0.5 | C. | x=2 | D. | x=1 |
 如图,在△ABC中,∠B=∠C,点D、E、F分别在AB、BC、AC上,且BD=CE,∠DEF=∠B,求证:△BDE≌△CEF.
如图,在△ABC中,∠B=∠C,点D、E、F分别在AB、BC、AC上,且BD=CE,∠DEF=∠B,求证:△BDE≌△CEF.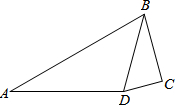 如图,在四边形ABCD中,∠A=30°,∠C=90°,∠ADB=105°,sin∠BDC=$\frac{{\sqrt{3}}}{2}$,AD=4.则DC的长=$\sqrt{2}$.
如图,在四边形ABCD中,∠A=30°,∠C=90°,∠ADB=105°,sin∠BDC=$\frac{{\sqrt{3}}}{2}$,AD=4.则DC的长=$\sqrt{2}$.