题目内容
6.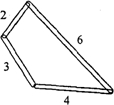 如图,用四个螺丝将四条不可弯曲的木条围成一个木框,不计螺丝大小,其中相邻两螺丝的距离依次为2、3、4、6,且相邻两木条的夹角均可调整.若调整木条的夹角时不破坏此木框,则任意两个螺丝间的距离的最大值为( )
如图,用四个螺丝将四条不可弯曲的木条围成一个木框,不计螺丝大小,其中相邻两螺丝的距离依次为2、3、4、6,且相邻两木条的夹角均可调整.若调整木条的夹角时不破坏此木框,则任意两个螺丝间的距离的最大值为( )| A. | 6 | B. | 7 | C. | 8 | D. | 10 |
分析 若两个螺丝的距离最大,则此时这个木框的形状为三角形,可根据三条木棍的长来判断有几种三角形的组合,然后分别找出这些三角形的最长边即可.
解答 解:已知4条木棍的四边长为2、3、4、6;
①选2+3、4、6作为三角形,则三边长为5、4、6;5-4<6<5+4,能构成三角形,此时两个螺丝间的最长距离为6;
②选3+4、6、2作为三角形,则三边长为2、7、6;6-2<7<6+2,能构成三角形,此时两个螺丝间的最大距离为7;
③选4+6、2、3作为三角形,则三边长为10、2、3;2+3<10,不能构成三角形,此种情况不成立;
④选6+2、3、4作为三角形,则三边长为8、3、4;而3+4<8,不能构成三角形,此种情况不成立;
综上所述,任两螺丝的距离之最大值为7.
故选:B.
点评 此题实际考查的是三角形的三边关系定理,能够正确的判断出调整角度后三角形木框的组合方法是解答的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11. 如图是函数y=$\frac{a}{x}$-1的图象,则关于x的分式方程$\frac{a}{x}$=3的解是( )
如图是函数y=$\frac{a}{x}$-1的图象,则关于x的分式方程$\frac{a}{x}$=3的解是( )
 如图是函数y=$\frac{a}{x}$-1的图象,则关于x的分式方程$\frac{a}{x}$=3的解是( )
如图是函数y=$\frac{a}{x}$-1的图象,则关于x的分式方程$\frac{a}{x}$=3的解是( )| A. | x=6 | B. | x=0.5 | C. | x=2 | D. | x=1 |
18.把一元二次方程x2-6x+4=0化成(x+n)2=m的形式时,m+n的值为( )
| A. | 8 | B. | 6 | C. | 3 | D. | 2 |
15.下列运算正确的是( )
| A. | 3a2-a2=2 | B. | a+a2=a3 | C. | (-2a)3=-8a3 | D. | a6÷a2=a3 |
16.下列运算正确的是( )
| A. | a6÷a2=a8 | B. | 3x2•5x3=15x5 | C. | (-3a2b)2=-6a4b2 | D. | (3a+b)(3a-b)=3a2-b2 |
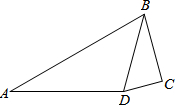 如图,在四边形ABCD中,∠A=30°,∠C=90°,∠ADB=105°,sin∠BDC=$\frac{{\sqrt{3}}}{2}$,AD=4.则DC的长=$\sqrt{2}$.
如图,在四边形ABCD中,∠A=30°,∠C=90°,∠ADB=105°,sin∠BDC=$\frac{{\sqrt{3}}}{2}$,AD=4.则DC的长=$\sqrt{2}$.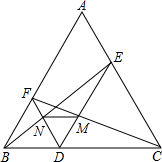 如图,点D是等边△ABC中BC边上一点,过点D分别作DE∥AB,DF∥AC,交AC,AB于E,F,连接BE,CF,分别交DF,DE于点N,M,连接MN.试判断△DMN的形状,并说明理由.
如图,点D是等边△ABC中BC边上一点,过点D分别作DE∥AB,DF∥AC,交AC,AB于E,F,连接BE,CF,分别交DF,DE于点N,M,连接MN.试判断△DMN的形状,并说明理由.