题目内容
5. 如图,直线l1∥l2,⊙O与l1和l2分别相切于点A和点B.直线MN与l1相交于M;与l2相交于N,⊙O的半径为1,∠1=60°,直线MN从如图位置向右平移,下列结论
如图,直线l1∥l2,⊙O与l1和l2分别相切于点A和点B.直线MN与l1相交于M;与l2相交于N,⊙O的半径为1,∠1=60°,直线MN从如图位置向右平移,下列结论①l1和l2的距离为2 ②MN=$\frac{4\sqrt{3}}{3}$ ③当直线MN与⊙O相切时,∠MON=90°
④当AM+BN=$\frac{4\sqrt{3}}{3}$时,直线MN与⊙O相切.正确的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 如图1,利用切线的性质得到OA⊥l1,OB⊥l2,再证明点A、B、O共线即可得到l1和l2的距离为2,则可对①进行判断;作NH⊥AM,如图1,易得四边形ABNH为矩形,则NH=AB=2,然后在Rt△MNH中利用含30度的直角三角形三边的关系可计算出MN,从而可对②进行判断;当直线MN与⊙O相切时,如图2,利用切线长定理得到∠1=∠2,∠3=∠4,然后根据平行线的性质和三角形内角和可计算出∠MON的度数,则可对③进行判断;过点O作OC⊥MN于C,如图2,根据梯形的面积和三角形面积公式,利用S四边形ABNM=S△OAM+S△OMN+S△OBN得到$\frac{1}{2}$•1•AM+$\frac{1}{2}$•1•BN+$\frac{1}{2}$MN•OC=$\frac{1}{2}$(BN+AM)•2,则根据AM+BN=$\frac{4\sqrt{3}}{3}$,MN=$\frac{4\sqrt{3}}{3}$可计算出OC=1,然后根据切线的判定定理可判断直线MN与⊙O相切,则可对④进行判断.
解答 解:如图1,∵⊙O与l1和l2分别相切于点A和点B,
∴OA⊥l1,OB⊥l2,
∵l1∥l2,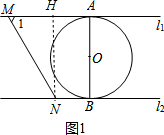
∴点A、B、O共线,
∴l1和l2的距离=AB=2,所以①正确;
作NH⊥AM,如图1,则四边形ABNH为矩形,
∴NH=AB=2,
在Rt△MNH中,∵∠1=60°,
∴MH=$\frac{\sqrt{3}}{3}$NH=$\frac{2\sqrt{3}}{3}$,
∴MN=2MH=$\frac{4\sqrt{3}}{3}$,所以②正确;
当直线MN与⊙O相切时,如图2,∠1=∠2,∠3=∠4,
∵l1∥l2,
∴∠1+∠2+∠3+∠4=180°,
∴∠1+∠3=90°,
∴∠MON=90°,所以③正确;
过点O作OC⊥MN于C,如图2,
∵S四边形ABNM=S△OAM+S△OMN+S△OBN,
∴$\frac{1}{2}$•1•AM+$\frac{1}{2}$•1•BN+$\frac{1}{2}$MN•OC=$\frac{1}{2}$(BN+AM)•2,
即$\frac{1}{2}$(AM+BN)+MN•OC=AM+BN,
∵AM+BN=$\frac{4\sqrt{3}}{3}$,MN=$\frac{4\sqrt{3}}{3}$,
∴OC=1,
而OC⊥MN,
∴直线MN与⊙O相切,所以④正确.
故选D.
点评 本题考查了切线的判定与性质:圆的切线垂直于经过切点的半径;经过半径的外端且垂直于这条半径的直线是圆的切线.常见的辅助线的:判定切线时“连圆心和直线与圆的公共点”或“过圆心作这条直线的垂线”; 有切线时,常常“遇到切点连圆心得半径”.

 阅读快车系列答案
阅读快车系列答案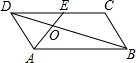 如图,在?ABCD中,E为CD的中点,AE交BD于点O,S△DCE=12,则S△AOD等于( )
如图,在?ABCD中,E为CD的中点,AE交BD于点O,S△DCE=12,则S△AOD等于( )| A. | 24 | B. | 36 | C. | 48 | D. | 60 |
| A. | 正方形 | B. | 矩形 | C. | 菱形 | D. | 平行四边形 |
 如图,现有一张矩形纸片(即矩形ABCD),若沿虚线剪去∠C,则∠1+∠2的度数为( )
如图,现有一张矩形纸片(即矩形ABCD),若沿虚线剪去∠C,则∠1+∠2的度数为( )| A. | 180° | B. | 240° | C. | 270° | D. | 330° |
 如图,在?ABCD中,对角线AC、BD相交于点O,点E是CD的中点,BC=12,则OE的长为6.
如图,在?ABCD中,对角线AC、BD相交于点O,点E是CD的中点,BC=12,则OE的长为6. 如图,菱形中,对角线AC、BD交于点O,E为AD边中点,菱形ABCD的周长为32,则OE的长等于( )
如图,菱形中,对角线AC、BD交于点O,E为AD边中点,菱形ABCD的周长为32,则OE的长等于( ) 如图,在△ABC中(AB>AC),AD是BC边上的高,E、F、G分别是BC、AB、AC三边的中点.
如图,在△ABC中(AB>AC),AD是BC边上的高,E、F、G分别是BC、AB、AC三边的中点. 如图,点C是线段AB上一点,点M、N、P分别是线段AC,BC,AB的中点.
如图,点C是线段AB上一点,点M、N、P分别是线段AC,BC,AB的中点.