题目内容
20.已知,等腰直角△ABC的斜边AB的坐标分别为:A(0,0)、B(12,0),且点C在第一象限,有一条直线经过点C,且与直线AB交于点D,如果点D将线段AB分成1:2的两段,那么求此直线的解析式?分析 根据△ABC为等腰直角三角形,以及点A、B的坐标和C点在第一象限,可得出C点的坐标为(6,6),由点D将线段AB分成1:2的两段,可找出点D的坐标为(4,0),设出直线CD的解析式,结合待定系数法可得出结论.
解答 解:依照题意画出图形,作CE⊥AB于E点,如下图所示.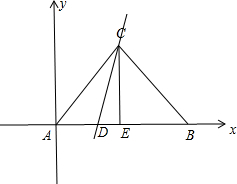
∵△ABC为等腰直角三角形,
∴有CE=AE=$\frac{1}{2}$AB,
∵A(0,0)、B(12,0),
∴CE=AE=6,
即点C的坐标为(6,6).
∵点D将线段AB分成1:2的两段,
∴AD=$\frac{1}{3}$AB=4,
即点D的坐标为(4,0).
设线段CD的解析式为y=kx+b,
由C、D点在直线上可知:$\left\{\begin{array}{l}{0=4k+b}\\{6=6k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=3}\\{b=-12}\end{array}\right.$.
故直线CD的解析式为y=3x-12.
点评 本题考查了等腰直角三角形的性质以及待定系数法求一次函数解析式,解题的关键是找出点C点D的坐标.本题属于基础题,难度不大,解决此类题型时,找点的坐标是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.关于抛物线y=x2-(a+1)x+a-2,下列说法错误的是( )
| A. | 开口向上 | B. | 当a=2时,经过坐标原点O | ||
| C. | a>0时,对称轴在y轴左侧 | D. | 不论a为何值,都经过定点(1,-2) |
9.在?ABCD中,AB=9cm,AD=4cm,∠C=50°,将这个平行四边形剪下,然后进行折叠,使AD落在AB上,折痕为AE,则有( )
| A. | ∠AEC=130° | B. | DE=4cm | C. | ∠B=150° | D. | EC=4cm |
 如图,将三角形纸片ABC沿DE折叠,使点A落在BC边上的点F处,且DE∥BC,当DE=2时,BC的长为( )
如图,将三角形纸片ABC沿DE折叠,使点A落在BC边上的点F处,且DE∥BC,当DE=2时,BC的长为( ) 如图(1)作∠ACB的角平分线(尺规作图);(2)在△ABC中,画出BC边的高.
如图(1)作∠ACB的角平分线(尺规作图);(2)在△ABC中,画出BC边的高.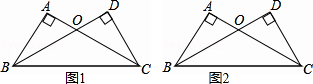
 在正方形ABCD中,点P是边BC上一动点(不包含端点),线段AP的垂直平分线与AB,AP,BD,AD分别交于点M,E,F,N.
在正方形ABCD中,点P是边BC上一动点(不包含端点),线段AP的垂直平分线与AB,AP,BD,AD分别交于点M,E,F,N.