题目内容
2. 如图,点A(1,4),B(-4,n)在双曲线y=$\frac{k}{x}$的图象上,直线AB分别交x轴、y轴于C,D,过点A作AE⊥x轴,垂足为E,过点B作BF⊥y轴,垂足为F,连接AF,BE交于点G.
如图,点A(1,4),B(-4,n)在双曲线y=$\frac{k}{x}$的图象上,直线AB分别交x轴、y轴于C,D,过点A作AE⊥x轴,垂足为E,过点B作BF⊥y轴,垂足为F,连接AF,BE交于点G.(1)求k的值及直线AB的解析式;
(2)判断四边形ADEF的形状,并写出证明过程.
分析 (1)根据反比例函数图象上点的坐标特征求出k,利用待定系数法求出直线AB的解析式;
(2)根据一组对边平行且相等的四边形是平行四边形证明即可.
解答 解:(1)∵点A(1,4)在双曲线y=$\frac{k}{x}$的图象上,
∴4=$\frac{k}{1}$,
解得k=4,
∴点B的坐标(-4,-1),
设直线AB的解析式为y=kx+b,
则$\left\{\begin{array}{l}{k+b=4}\\{-4k+b=-1}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{k=1}\\{b=3}\end{array}\right.$,
∴直线AB的解析式为y=x+3;
(2)直线AB的解析式为y=x+3与y轴的交点D的坐标为(0,3),
∴OD=3,又OF=1,
∴DF=4,又AE=4,
∴AE=DF,
∵AE∥DF,
∴四边形ADEF是平行四边形.
点评 本题考查的是一次函数与反比例函数的交点、平行四边形的判定,掌握待定系数法求函数解析式的一般步骤、掌握平行四边形的判定定理是解题的关键.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
10.关于抛物线y=x2-(a+1)x+a-2,下列说法错误的是( )
| A. | 开口向上 | B. | 当a=2时,经过坐标原点O | ||
| C. | a>0时,对称轴在y轴左侧 | D. | 不论a为何值,都经过定点(1,-2) |
 两位同学玩“石头、剪子、布”游戏,随机出手一次,两人手势相同的概率是$\frac{1}{3}$.
两位同学玩“石头、剪子、布”游戏,随机出手一次,两人手势相同的概率是$\frac{1}{3}$.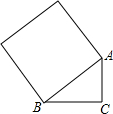 如图,∠ACB=90°,AC=3,BC=4,则以AB为边长的正方形面积为25.
如图,∠ACB=90°,AC=3,BC=4,则以AB为边长的正方形面积为25. 如图,将三角形纸片ABC沿DE折叠,使点A落在BC边上的点F处,且DE∥BC,当DE=2时,BC的长为( )
如图,将三角形纸片ABC沿DE折叠,使点A落在BC边上的点F处,且DE∥BC,当DE=2时,BC的长为( )