题目内容
20.如图A、B在方格纸的格点位置上.(1)若要再找一个格点C,使△ABC为等腰三角形,则这样的格点C在图中共有10个;
(2)若要再找一个格点D,使△ABD的面积为3,则这样的格点D在图中共有8个;
(3)若要再找一个个点E,使△ABE的三边均为无理数,则这样的格点E在图中共有16个.
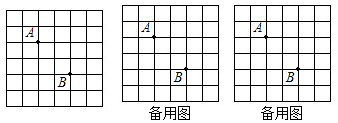
分析 (1)根据勾股定理计算出AB=2$\sqrt{2}$,然后分类讨论确定C点位置;
(2)找到△ABD的面积为3的格点即为所求;
(3)本题需根据勾股定理和图形即可找出所有满足条件的点..
解答 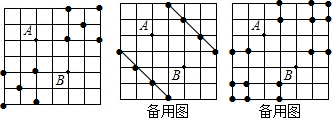 解:(1)如图所示:
解:(1)如图所示:
AB=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
以B为顶点,BC=BA,这样的C点有2个;
以A为顶点,AC=AB,这样的C点有2个;
以C为顶点,CA=CB,这样的点有6个,
所以使△ABC的等腰三角形,这样的格点C的个数有10个.
(2)如图所示:
若要再找一个格点D,使△ABD的面积为3,则这样的格点D在图中共有8个.
(3)如图所示:
若要再找一个个点E,使△ABE的三边均为无理数,则这样的格点E在图中共有16个,
故答案为:10;8;16.
点评 本题考查了勾股定理;熟练掌握勾股定理,并能进行推理计算与作图是解决问题的关键.

练习册系列答案
相关题目
11.下列关于x的一元二次方程没有实数根的是( )
| A. | x2=3 | B. | x2=x | C. | x2+x+1=0 | D. | x2-x-1=0 |
10.下列计算结果是-3是( )
| A. | (-3)×(-1) | B. | (-3)2÷3 | C. | -|-3| | D. | -(-3) |
 已知:二次函数y=-x2+bx+c的图象过点(-1,-8),(0,-3).
已知:二次函数y=-x2+bx+c的图象过点(-1,-8),(0,-3).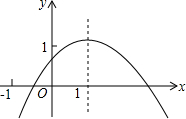 如图,二次函数y=ax2+bx+c的图象的对称轴是直线x=1,则下列结论:
如图,二次函数y=ax2+bx+c的图象的对称轴是直线x=1,则下列结论:
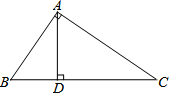 如图,在△ABC中∠BAC=90°,AB=15,AC=20,AD⊥BC,垂足为D,则BD的长为9.
如图,在△ABC中∠BAC=90°,AB=15,AC=20,AD⊥BC,垂足为D,则BD的长为9.