题目内容
10. 已知:二次函数y=-x2+bx+c的图象过点(-1,-8),(0,-3).
已知:二次函数y=-x2+bx+c的图象过点(-1,-8),(0,-3).(1)求此二次函数的表达式,并用配方法将其化为y=a(x-h)2+k的形式;
(2)用五点法画出此函数图象的示意图.
分析 (1)把已知两点(-1,-8),(0,-3)代入二次函数的解析式求出b和c的值,再配方成顶点式;
(2)写出顶点坐标,计算其与x轴的交点和与y轴的交点,列表、描点,画出图象.
解答 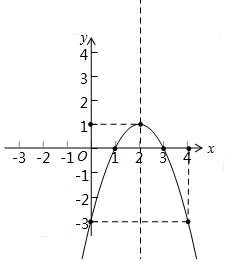 解:(1)把(-1,-8),(0,-3)代入y=-x2+bx+c得:$\left\{\begin{array}{l}{-1-b+c=-8}\\{c=-3}\end{array}\right.$,
解:(1)把(-1,-8),(0,-3)代入y=-x2+bx+c得:$\left\{\begin{array}{l}{-1-b+c=-8}\\{c=-3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=4}\\{c=-3}\end{array}\right.$,
∴二次函数的表达式为:y=-x2+4x-3,
y=-x2+4x-3=-(x-2)2+1;
(2)顶点(2,1),
当y=0时,-x2+4x-3=0,
x2-4x+3=0,
(x-1)(x-3)=0,
x1=1,x2=3,
∴与x轴交点为(1,0)、(3,0),
列表如下: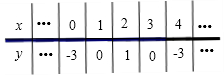
点评 本题考查了利用待定系数法求二次函数的解析式和画出二次函数的图象,知道用五点法画二次函数图象的方法:①五点是指:顶点、与x轴的两个交点、与y轴交点及其对称点(也可取任意两个对称点),②计算出五点的坐标,③再列表、描点,连线即可.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案
相关题目
20.下面三条线段(单位:厘米)可以构成三角形的是( )
| A. | 1、2、3 | B. | 2、3、4 | C. | 5、7、13 | D. | 2、5、8 |