题目内容
12.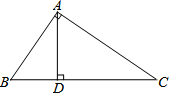 如图,在△ABC中∠BAC=90°,AB=15,AC=20,AD⊥BC,垂足为D,则BD的长为9.
如图,在△ABC中∠BAC=90°,AB=15,AC=20,AD⊥BC,垂足为D,则BD的长为9.
分析 先根据勾股定理求出BC,再根据三角形面积公式得出AB×AC=BC×AD,代入求出AD,再根据勾股定理求出BD即可.
解答 解:利用勾股定理:BC=$\sqrt{A{B}^{2}+A{C}^{2}}$=25;
∵S△ACB=$\frac{1}{2}$×AB×AC=$\frac{1}{2}$×BC×AD,
∴15×20=25×AD,
∴AD=12,
利用勾股定理:BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=9.
故答案为:9.
点评 本题考查了三角形面积和勾股定理的应用,注意:在直角三角形中,两直角边的平方和等于斜边的平方.

练习册系列答案
相关题目
7.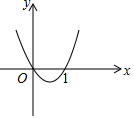 如图为二次函数y=ax2+bx+c的图象,下列各式中:①a>0,②b>0,③c=0,④c=1,⑤a+b+c=0.正确的只有( )
如图为二次函数y=ax2+bx+c的图象,下列各式中:①a>0,②b>0,③c=0,④c=1,⑤a+b+c=0.正确的只有( )
 如图为二次函数y=ax2+bx+c的图象,下列各式中:①a>0,②b>0,③c=0,④c=1,⑤a+b+c=0.正确的只有( )
如图为二次函数y=ax2+bx+c的图象,下列各式中:①a>0,②b>0,③c=0,④c=1,⑤a+b+c=0.正确的只有( )| A. | ①④ | B. | ②③④ | C. | ③④⑤ | D. | ①③⑤ |
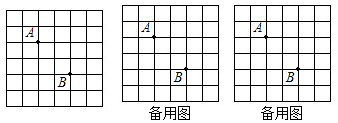
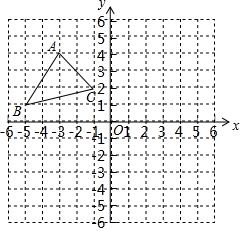 如图,在平面直角坐标系xOy中,△ABC的三个顶点分别为A(-3,4),B(-5,1),C(-1,2).
如图,在平面直角坐标系xOy中,△ABC的三个顶点分别为A(-3,4),B(-5,1),C(-1,2). 如图,已知A、B、C、D是⊙O上的四点,若∠BOD=100°,则∠C=130°.
如图,已知A、B、C、D是⊙O上的四点,若∠BOD=100°,则∠C=130°.