题目内容
10.已知AD是△ABC的高,∠ABC=30°,∠CAD=50°,则∠BAC的度数为40°.分析 在Rt△ABD中,∠B与∠BAD互余,而∠CAD=20°,故有∠BAC=∠BAD-∠CAD.
解答 解:如图,
∵∠D=90°,∠B=30°,
∴∠BAD=60°,
∵∠CAD=20°,
∴∠BAC=∠BAD-∠CAD=60°-20°=40°.
故答案为:40°.
点评 此题考查三角形的内角和,直角三角形两个锐角互余的性质,把问题转化为两个角的差解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.下列运算正确的是( )
| A. | 4$\sqrt{3}$-3$\sqrt{3}$=1 | B. | $\sqrt{2}$$+\sqrt{3}$=$\sqrt{5}$ | C. | $\frac{\sqrt{8}}{\sqrt{2}}$=2 | D. | $\sqrt{(-3)^{2}}$=-3 |
18.⊙O中,∠AOB=80°,若C是⊙O上一点(不与A、B重合),则∠ACB等于( )
| A. | 40° | B. | 80° | C. | 80°或100° | D. | 40°或140° |
5.若xa=3,xb=5,则x3a-2b的值为( )
| A. | $\frac{27}{25}$ | B. | $\frac{3}{5}$ | C. | 2 | D. | 52 |
15.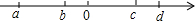 有理数a、b、c、d在数轴上的位置如图所示,下列结论中错误的是( )
有理数a、b、c、d在数轴上的位置如图所示,下列结论中错误的是( )
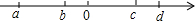 有理数a、b、c、d在数轴上的位置如图所示,下列结论中错误的是( )
有理数a、b、c、d在数轴上的位置如图所示,下列结论中错误的是( )| A. | a+b<0 | B. | c+d>0 | C. | |a+c|=a+c | D. | |b+d|=b+d |
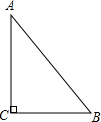 如图,在Rt△ABC中,斜边AB=5,直角边BC=$\sqrt{5}$,求三角形的面积.
如图,在Rt△ABC中,斜边AB=5,直角边BC=$\sqrt{5}$,求三角形的面积.