题目内容
20．
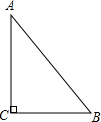如图，在Rt△ABC中，斜边AB=5，直角边BC=$\sqrt{5}$，求三角形的面积．
分析 先根据勾股定理求出AC的长，再由三角形的面积公式即可得出结论．
解答 解：∵在Rt△ABC中，斜边AB=5，直角边BC=$\sqrt{5}$，
∴AC=$\sqrt{{AB}^{2}-{BC}^{2}}$=$\sqrt{{5}^{2}-{（\sqrt{5}）}^{2}}$=2$\sqrt{5}$，
∴S△ABC=$\frac{1}{2}$BC•AC=$\frac{1}{2}$×$\sqrt{5}$×2$\sqrt{5}$=5．
点评 本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．
练习册系列答案
相关题目
18．如图，函数y=-x（x＜0）的图象是（ ）
| A． |  | B． |  | C． |  | D． |  |
11．某单位招聘员工，采取笔试与面试相结合的方式进行，两项成绩的原始分均为100分．前5名选手的得分如下：
根据规定，笔试成绩和面试成绩分别占总成绩的40%和60%．
（1）这5名选手笔试成绩的中位数是84分，众数是84分．
（2）现得知1号、2号、3号选手的综合成绩分别为88分、85.2分、81.6分，求出其余两名选手的综合成绩，并确定谁将被录取？
| 序号项目 | 1 | 2 | 3 | 4 | 5 |
| 笔试成绩/分 | 85 | 84 | 84 | 90 | 80 |
| 面试成绩/分 | 90 | 86 | 80 | 90 | 85 |
（1）这5名选手笔试成绩的中位数是84分，众数是84分．
（2）现得知1号、2号、3号选手的综合成绩分别为88分、85.2分、81.6分，求出其余两名选手的综合成绩，并确定谁将被录取？
8．
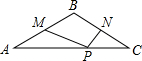如图，在等腰三角形ABC中，∠ABC=120°，点P是底边AC上的一个动点，M、N分别是AB、BC的中点，若PM+PN的最小值为2，则△ABC的周长是（ ）
如图，在等腰三角形ABC中，∠ABC=120°，点P是底边AC上的一个动点，M、N分别是AB、BC的中点，若PM+PN的最小值为2，则△ABC的周长是（ ）| A． | 2+$\sqrt{3}$ | B． | 4 | C． | 4+2$\sqrt{3}$ | D． | 12 |
