题目内容
 如图,在△ABC中,AB=AC,BD是AC边上的高,过点A作直线L,分别过B、C作BE⊥L,CF⊥L,E、F是垂足.证明:
如图,在△ABC中,AB=AC,BD是AC边上的高,过点A作直线L,分别过B、C作BE⊥L,CF⊥L,E、F是垂足.证明:(1)A、E、B、D四点共圆;
(2)DE=CF.
考点:四点共圆
专题:证明题
分析:(1)取AB的中点O,连接OE、OD,根据直角三角形斜边上的中线等于斜边的一半可得OE=OA=OB=OD,即可得到A、E、B、D四点共圆.
(2)根据正弦定理可得
=AB,根据圆内接四边形的性质可得∠FAC=∠EBD,从而有sin∠FAC=
,在Rt△FAC中,根据三角函数的定义可得sin∠FAC=
,从而有
=
.由AB=AC就可得到ED=FC.
(2)根据正弦定理可得
| ED |
| sin∠EBD |
| ED |
| AB |
| FC |
| AC |
| ED |
| AB |
| FC |
| AC |
解答: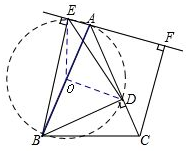 证明:(1)取AB的中点O,连接OE、OD,如图.
证明:(1)取AB的中点O,连接OE、OD,如图.
∵BE⊥EA,BD⊥AC,
∴∠BEA=∠ADB=90°.
∵点O为AB的中点,
∴OE=OA=OB=OD,
∴A、E、B、D在以AB为直径的圆上,
即A、E、B、D四点共圆.
(2)如图,
∵四边形AEBD是以AB为直径的圆内接四边形,
∴
=AB(正弦定理),∠FAC=∠EBD,
∴sin∠FAC=
.
在Rt△FAC中,有sin∠FAC=
,
∴
=
.
∵AB=AC,
∴ED=FC.
 证明:(1)取AB的中点O,连接OE、OD,如图.
证明:(1)取AB的中点O,连接OE、OD,如图.∵BE⊥EA,BD⊥AC,
∴∠BEA=∠ADB=90°.
∵点O为AB的中点,
∴OE=OA=OB=OD,
∴A、E、B、D在以AB为直径的圆上,
即A、E、B、D四点共圆.
(2)如图,
∵四边形AEBD是以AB为直径的圆内接四边形,
∴
| ED |
| sin∠EBD |
∴sin∠FAC=
| ED |
| AB |
在Rt△FAC中,有sin∠FAC=
| FC |
| AC |
∴
| ED |
| AB |
| FC |
| AC |
∵AB=AC,
∴ED=FC.
点评:本题考查了四点共圆的判定、直角三角形斜边上的中线等于斜边的一半、圆内接四边形的性质、正弦定理、三角函数的定义等知识,运用正弦定理及圆内接四边形的性质则是解决第(2)小题的关键.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目
若2x+2y=xy,则
+
的值为( )
| 1 |
| x |
| 1 |
| y |
| A、0 | ||
| B、-1 | ||
C、
| ||
| D、2 |
实数 -
,-2,-3的大小关系是( )
| 7 |
A、-
| ||
B、-3<-
| ||
C、-2<-
| ||
D、-3<-2<-
|
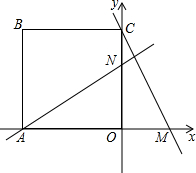 如图,将边长为4的正方形ABCO放置在直角坐标系中,使点A在x轴负半轴上,点C在y轴正半轴上.点M(t,0)在x正半轴上运动,过A作直线MC的垂线交y轴于点N.下列结论:
如图,将边长为4的正方形ABCO放置在直角坐标系中,使点A在x轴负半轴上,点C在y轴正半轴上.点M(t,0)在x正半轴上运动,过A作直线MC的垂线交y轴于点N.下列结论: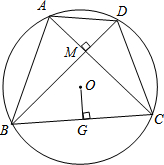 已知:圆的内接四边形ABCD的对角线AC和BD互相垂直,OG⊥BC,求证:OG=
已知:圆的内接四边形ABCD的对角线AC和BD互相垂直,OG⊥BC,求证:OG=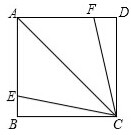 如图,AC是正方形ABCD的对角线,E、F分别为AB、AD边上的点,且AE=AF,连接CE、CF.
如图,AC是正方形ABCD的对角线,E、F分别为AB、AD边上的点,且AE=AF,连接CE、CF.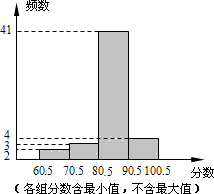 某中学在一次健康知识测试中,抽取部分学生的成绩(分数为整数,满分100分)为样本,绘制成绩统计图如图所示,请结合统计图回答下列问题:
某中学在一次健康知识测试中,抽取部分学生的成绩(分数为整数,满分100分)为样本,绘制成绩统计图如图所示,请结合统计图回答下列问题: