题目内容
已知抛物线y=ax2+bx+c(a<0)交x轴于点A(-3,0)、B(1,0),交y轴于点C,顶点为P,以PA为直径的⊙D恰好过点C.
(1)求该抛物线的解析式;
(2)抛物线的对称轴、顶点坐标;
(3)求当x为何值时,y随x的增大而减小?
(1)求该抛物线的解析式;
(2)抛物线的对称轴、顶点坐标;
(3)求当x为何值时,y随x的增大而减小?
考点:二次函数综合题
专题:
分析:(1)由抛物线y=ax2+bx+c(a<0)交x轴于点A(-3,0)、B(1,0),可得b=2a,c=-3a,对称轴为直线x=-1,又由以PA为直径的⊙D恰好过点C,可得∠ACP=90°,然后由勾股定理得到方程:(3-1)2+(4a)2=[32+(3a)2]+[12+(4a-3a)2],解此方程即可求得答案;
(2)利用配方法即可求得抛物线的对称轴、顶点坐标;
(3)根据图象即可求得当x为何值时,y随x的增大而减小.
(2)利用配方法即可求得抛物线的对称轴、顶点坐标;
(3)根据图象即可求得当x为何值时,y随x的增大而减小.
解答: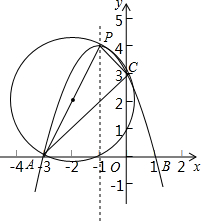 解:(1)如图,∵抛物线y=ax2+bx+c(a<0)交x轴于点A(-3,0)、B(1,0),
解:(1)如图,∵抛物线y=ax2+bx+c(a<0)交x轴于点A(-3,0)、B(1,0),
∴
,
∴
,
∵以PA为直径的⊙D恰好过点C,
∴∠ACP=90°,
∴AP2=AC2+PC2,
∵抛物线y=ax2+bx+c(a<0)交x轴于点A(-3,0)、B(1,0),
∴抛物线y=ax2+bx+c的对称轴为直线x=-1,
∴点P(-1,a-b+c)即(-1,-4a),
∵抛物线y=ax2+bx+c(a<0)交y轴于点C,
∴点C(0,c),即(0,-3a),
∴(3-1)2+(4a)2=[32+(3a)2]+[12+(4a-3a)2],
解得:a=±1,
∵a<0,
∴a=-1,
∴b=-2,c=3,
∴该抛物线的解析式为:y=-x2-2x+3;
(2)∵y=-x2-2x+3=-(x+1)2+4,
∴抛物线的对称轴为直线x=-1,顶点坐标为(-1,4);
(3)如图,当x>-1时,y随x的增大而减小.
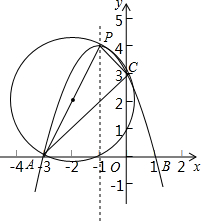 解:(1)如图,∵抛物线y=ax2+bx+c(a<0)交x轴于点A(-3,0)、B(1,0),
解:(1)如图,∵抛物线y=ax2+bx+c(a<0)交x轴于点A(-3,0)、B(1,0),∴
|
∴
|
∵以PA为直径的⊙D恰好过点C,
∴∠ACP=90°,
∴AP2=AC2+PC2,
∵抛物线y=ax2+bx+c(a<0)交x轴于点A(-3,0)、B(1,0),
∴抛物线y=ax2+bx+c的对称轴为直线x=-1,
∴点P(-1,a-b+c)即(-1,-4a),
∵抛物线y=ax2+bx+c(a<0)交y轴于点C,
∴点C(0,c),即(0,-3a),
∴(3-1)2+(4a)2=[32+(3a)2]+[12+(4a-3a)2],
解得:a=±1,
∵a<0,
∴a=-1,
∴b=-2,c=3,
∴该抛物线的解析式为:y=-x2-2x+3;
(2)∵y=-x2-2x+3=-(x+1)2+4,
∴抛物线的对称轴为直线x=-1,顶点坐标为(-1,4);
(3)如图,当x>-1时,y随x的增大而减小.
点评:此题考查了待定系数法求二次函数的解析式、圆周角定理以及勾股定理等知识.此题难度较大,综合性较强,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
相关题目
 如图,直线y=-
如图,直线y=-| 3 |
| 4 |
| A、3≤m≤4 | ||
| B、2≤m≤4 | ||
C、0≤m≤
| ||
| D、0≤m≤3 |
 如图,把一块直角三角板ABC绕着30°角的顶点B顺时针旋转,使得点A与CB的延长线上的点E重合.
如图,把一块直角三角板ABC绕着30°角的顶点B顺时针旋转,使得点A与CB的延长线上的点E重合. 如图,在△ABC中,AB=AC,BD是AC边上的高,过点A作直线L,分别过B、C作BE⊥L,CF⊥L,E、F是垂足.证明:
如图,在△ABC中,AB=AC,BD是AC边上的高,过点A作直线L,分别过B、C作BE⊥L,CF⊥L,E、F是垂足.证明: