题目内容
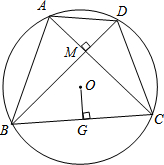 已知:圆的内接四边形ABCD的对角线AC和BD互相垂直,OG⊥BC,求证:OG=
已知:圆的内接四边形ABCD的对角线AC和BD互相垂直,OG⊥BC,求证:OG=| 1 |
| 2 |
考点:三角形中位线定理,圆心角、弧、弦的关系,圆周角定理
专题:证明题
分析:如图,连接BO并延长BO交圆O于E,连接AE、DE.构建OG是△BCE的中位线,由三角形中位线定理证得结论.
解答: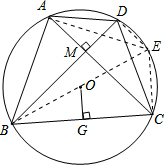 证明:如图,连接BO并延长BO交圆O于E,连接AE、DE、EC.
证明:如图,连接BO并延长BO交圆O于E,连接AE、DE、EC.
∵BE是直径,
∴∠BAE=∠BDE=90°.
∵AC⊥BD,
∴AC∥DE,
∴
=
.
∵
=
+
,
=
+
,
∴
=
,
∴AD=CE.
∵G为BC中点,OB=OE,
∴OG是△BCE的中位线,
∴OG=
CE,
∴OG=
AD.
 证明:如图,连接BO并延长BO交圆O于E,连接AE、DE、EC.
证明:如图,连接BO并延长BO交圆O于E,连接AE、DE、EC.∵BE是直径,
∴∠BAE=∠BDE=90°.
∵AC⊥BD,
∴AC∥DE,
∴
 |
| AD |
 |
| CE |
∵
 |
| AE |
 |
| AD |
 |
| DE |
 |
| CD |
 |
| CE |
 |
| DE |
∴
 |
| AE |
 |
| CD |
∴AD=CE.
∵G为BC中点,OB=OE,
∴OG是△BCE的中位线,
∴OG=
| 1 |
| 2 |
∴OG=
| 1 |
| 2 |
点评:本题考查了三角形中位线定理,圆周角定理以及圆心角、弧、弦的关系.解答此题的关键是根据题意作出辅助线.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
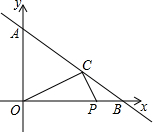 如图,直线y=-
如图,直线y=-| 3 |
| 4 |
| A、3≤m≤4 | ||
| B、2≤m≤4 | ||
C、0≤m≤
| ||
| D、0≤m≤3 |
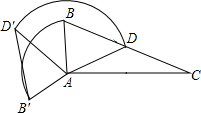 Rt△ABC中,∠BAC=90°,BC=6,点D为BC的中点,将△ABD绕点A按逆时针方向旋转120°得到△AB′D′,则点D在旋转过程中所经过的路程是多少?(结果保留π)
Rt△ABC中,∠BAC=90°,BC=6,点D为BC的中点,将△ABD绕点A按逆时针方向旋转120°得到△AB′D′,则点D在旋转过程中所经过的路程是多少?(结果保留π) 如图,在△ABC中,AB=AC,BD是AC边上的高,过点A作直线L,分别过B、C作BE⊥L,CF⊥L,E、F是垂足.证明:
如图,在△ABC中,AB=AC,BD是AC边上的高,过点A作直线L,分别过B、C作BE⊥L,CF⊥L,E、F是垂足.证明: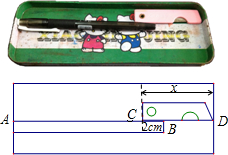 如图,在铅笔盒中有一支圆珠笔和一把小刀,已知圆珠笔的长AB是小刀长CD(小刀不打开时的最大长度)的
如图,在铅笔盒中有一支圆珠笔和一把小刀,已知圆珠笔的长AB是小刀长CD(小刀不打开时的最大长度)的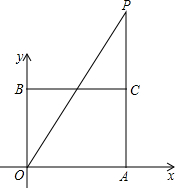 如图,长方形AOBC在直角坐标系中,A、B两点坐标分别为(8,0)、(0,6),点P是长方形一边所在直线上的一个动点,并且它位于y轴右侧.
如图,长方形AOBC在直角坐标系中,A、B两点坐标分别为(8,0)、(0,6),点P是长方形一边所在直线上的一个动点,并且它位于y轴右侧.