题目内容
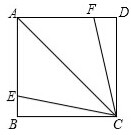如图，AC是正方形ABCD的对角线，E、F分别为AB、AD边上的点，且AE=AF，连接CE、CF．（1）求证：CE=CF；
（2）若∠BCE=30°，求
| AE |
| AB |
考点：正方形的性质,全等三角形的判定与性质
专题：
分析：（1）证得△ACE≌△ACF，即可得出结论；
（2）利用特殊角的三角函数值求得BE=AB•tan30°=
AB，进一步表示出AE=AB-BE=
AB，进一步得出结论即可．
（2）利用特殊角的三角函数值求得BE=AB•tan30°=
| ||
| 3 |
3-
| ||
| 3 |
解答：（1）证明：∵四边形ABCD是正方形，
∴AB=BC，∠BAC=∠DAC，
在△ACE和△ACF中，
，
∴△ACE≌△ACF（SAS），
∴CE=CF．
（2）解：∵∠BCE=30°，∠B=90°，
∴BE=AB•tan30°=
AB，
∴AE=AB-BE=
AB，
∴
=
．
∴AB=BC，∠BAC=∠DAC，
在△ACE和△ACF中，
|
∴△ACE≌△ACF（SAS），
∴CE=CF．
（2）解：∵∠BCE=30°，∠B=90°，
∴BE=AB•tan30°=
| ||
| 3 |
∴AE=AB-BE=
3-
| ||
| 3 |
∴
| AE |
| AB |
3-
| ||
| 3 |
点评：此题考查了正方形的性质、解直角三角形、三角形全等的判定与性质等知识．
练习册系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
如图，在△ABC中，AB=AC，BD是AC边上的高，过点A作直线L，分别过B、C作BE⊥L，CF⊥L，E、F是垂足．证明：
如图所示，可以看作是正方形ABCD绕点O分别旋转多少度前后的图形共同组成的（ ）| A、30°，45° |
| B、60°，45° |
| C、45°，90° |
| D、22.5°，67.5° |
一袋小麦以每袋150千克为准，超过的千克数记为正数，不足的千克数记为负数，分别记为：-6，4，3，-2，-3，1，0，5，8，-5，与标准质量相比较，这10袋小麦总计超过或不足多少千克？10袋小麦总质量是多少千克？