��Ŀ����
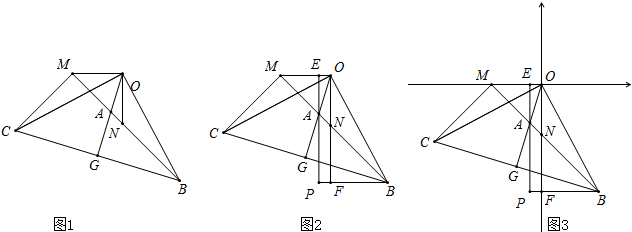
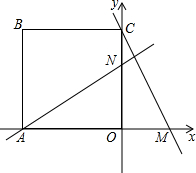 ��ͼ�����߳�Ϊ4��������ABCO������ֱ������ϵ�У�ʹ��A��x�Ḻ�����ϣ���C��y���������ϣ���M��t��0����x���������˶�����A��ֱ��MC�Ĵ��߽�y���ڵ�N�����н��ۣ�
��ͼ�����߳�Ϊ4��������ABCO������ֱ������ϵ�У�ʹ��A��x�Ḻ�����ϣ���C��y���������ϣ���M��t��0����x���������˶�����A��ֱ��MC�Ĵ��߽�y���ڵ�N�����н��ۣ���CM=AN��
�ڵ�t=4
| 2 |
�����Ե�A��M��N���㹹�ɵ��������ǵ��������Σ����M��������M��4
| 2 |
�ܵ���M��������M��8��0��ʱ����B��M��N���㹹�ɵ���������ֱ�������Σ�
������ȷ����
���㣺һ�κ����ۺ���
ר�⣺
��������֤����AON�ա�COM�����ɵõ�CM=AN��
������AC�����ù��ɶ������AC=AM�����жϳ���ACM�ǵ��������Σ�
�۾ٳ�������M��4��0��ʱ��CM=AC=4
��A��M��N���㹹�ɵ��������ǵ��������Σ�
�����ù��ɶ������BN2=42+42=16��MN2=82+82=128��BM2=42+122=160���жϳ�BN2+MN2=BM2���õ���B��M��N���㹹�ɵ���������ֱ�������Σ�
������AC�����ù��ɶ������AC=AM�����жϳ���ACM�ǵ��������Σ�
�۾ٳ�������M��4��0��ʱ��CM=AC=4
| 2 |
�����ù��ɶ������BN2=42+42=16��MN2=82+82=128��BM2=42+122=160���жϳ�BN2+MN2=BM2���õ���B��M��N���㹹�ɵ���������ֱ�������Σ�
����⣺�١ߡ�NCP+��CNP=90�㣬��NAO+��ANO=90�㣬��CNP=��ANO��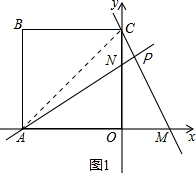
���NCP=��NAO��
��AO=CO����AON=��COM��
���AON�ա�COM��
��CM=AN���ʱ�ѡ����ȷ��
����ͼ1������AC����AO=4��OC=4��
��AC=
=4
��
��AM=AO+OM=4+4
-4=4
��
���ACM�ǵ��������Σ�
��ֱ��AN��ֱƽ���߶�CM���ʱ�ѡ����ȷ��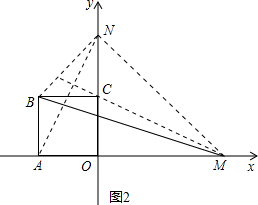
�۵�M��4��0��ʱ��CM=AC=4
��A��M��N���㹹�ɵ��������ǵ��������Σ��ʱ�ѡ�����
����ͼ2������M��������M��8��0��ʱ��MC�Ľ���ʽ��y=-
x+4��
AN�Ľ���ʽ��y=2x+8���ɵ�N��0��8����
��BN2=42+42=16��
MN2=82+82=128��
BM2=42+122=160��
��BN2+MN2=BM2��
����B��M��N���㹹�ɵ���������ֱ�������Σ��ʱ�ѡ����ȷ��
�ʴ�Ϊ�٢ڢܣ�

���NCP=��NAO��
��AO=CO����AON=��COM��
���AON�ա�COM��
��CM=AN���ʱ�ѡ����ȷ��
����ͼ1������AC����AO=4��OC=4��
��AC=
| 42+42 |
| 2 |
��AM=AO+OM=4+4
| 2 |
| 2 |
���ACM�ǵ��������Σ�
��ֱ��AN��ֱƽ���߶�CM���ʱ�ѡ����ȷ��

�۵�M��4��0��ʱ��CM=AC=4
| 2 |
����ͼ2������M��������M��8��0��ʱ��MC�Ľ���ʽ��y=-
| 1 |
| 2 |
AN�Ľ���ʽ��y=2x+8���ɵ�N��0��8����
��BN2=42+42=16��
MN2=82+82=128��
BM2=42+122=160��
��BN2+MN2=BM2��
����B��M��N���㹹�ɵ���������ֱ�������Σ��ʱ�ѡ����ȷ��
�ʴ�Ϊ�٢ڢܣ�
���������⿼����һ�κ����ۺ��⣬��Ϥһ�κ��������ʡ����������ε��ж������ʡ����ɶ����ǽ���Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
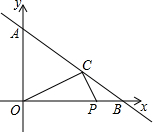 ��ͼ��ֱ��y=-
��ͼ��ֱ��y=-| 3 |
| 4 |
| A��3��m��4 | ||
| B��2��m��4 | ||
C��0��m��
| ||
| D��0��m��3 |
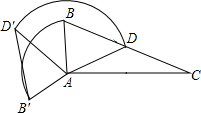 Rt��ABC�У���BAC=90�㣬BC=6����DΪBC���е㣬����ABD�Ƶ�A����ʱ�뷽����ת120��õ���AB��D�䣬���D����ת��������������·���Ƕ��٣�����������У�
Rt��ABC�У���BAC=90�㣬BC=6����DΪBC���е㣬����ABD�Ƶ�A����ʱ�뷽����ת120��õ���AB��D�䣬���D����ת��������������·���Ƕ��٣�����������У� ��ͼ���ڡ�ABC�У�AB=AC��BD��AC���ϵĸߣ�����A��ֱ��L���ֱ��B��C��BE��L��CF��L��E��F�Ǵ��㣮֤����
��ͼ���ڡ�ABC�У�AB=AC��BD��AC���ϵĸߣ�����A��ֱ��L���ֱ��B��C��BE��L��CF��L��E��F�Ǵ��㣮֤���� �������ϱ�ʾ�����и���������-2��-3
�������ϱ�ʾ�����и���������-2��-3