题目内容
4.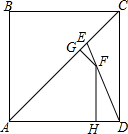 如图,已知正方形ABCD的边长为1,对角线AC上有一点E,使得AE=$\frac{{\sqrt{2}}}{2}$AC.连结DE,过线段DE上的一个动点F分别向AC和AD作垂线段,垂足分别为G、H.
如图,已知正方形ABCD的边长为1,对角线AC上有一点E,使得AE=$\frac{{\sqrt{2}}}{2}$AC.连结DE,过线段DE上的一个动点F分别向AC和AD作垂线段,垂足分别为G、H.(1)证明:△FGE∽△FHD;
(2)设线段FG的长度为x,线段FH的长度为y,求出y关于x的函数表达式,并写出自变量的取值范围;
(3)连结GH,求出△GHF面积的最大值.
分析 (1)首先利用勾股定理求得AC的长度,然后可求得AE=AD=1,从而可得到:∠AED=∠ADE,因为∠FGE=∠FHD=90°,故此可证明△FGE∽△FHD;
(2)首先证明△AEK∽△ACD,从而可知$\frac{AE}{AC}=\frac{EK}{DC}$,可求得EK=$\frac{\sqrt{2}}{2}$,然后根据△AED的面积=△AEF的面积+△ADF的面积可求得:FG+HF=$\frac{\sqrt{2}}{2}$,从而可求得y与x的函数关系式;
(3)首先在四边形AGFH中,求得∠GFH=135°,从而得到∠MFG=45°,然后利用特殊锐角三角形函数值可求得GM=$\frac{{\sqrt{2}}}{2}x$,从而可得到△GFH的面积与x的函数关系,最后利用配方法求得△GHF面积的最大值为$\frac{{\sqrt{2}}}{32}$.
解答 解:(1)如图1: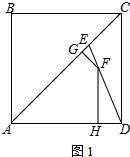
证明:在Rt△ABC中,AC=$\sqrt{{AB}^{2}+B{C}^{2}}=\sqrt{{1}^{2}+{1}^{2}}=\sqrt{2}$,
∴AE=$\frac{\sqrt{2}}{2}×\sqrt{2}$=1.
∵AE=AD=1,
∴∠AED=∠ADE.
又∵∠FGE=∠FHD=90°
∴△FGE∽△FHD
(2)如图2:连接AF,过点E作Ek⊥AD,垂足为k.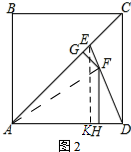
∵EK⊥AD,DC⊥AD,
∴EK∥DC.
∴△AEK∽△ACD.
∴$\frac{AE}{AC}=\frac{EK}{DC}$即:$\frac{1}{\sqrt{2}}=\frac{EK}{1}$.
∴EK=$\frac{\sqrt{2}}{2}$.
∴△AED的面积=$\frac{1}{2}AD•EK=\frac{1}{2}×1×\frac{\sqrt{2}}{2}$=$\frac{\sqrt{2}}{4}$
∵△AED的面积=△AEF的面积+△ADF的面积
=$\frac{1}{2}AE•FG+\frac{1}{2}AD•FH$
=$\frac{1}{2}×1×FG+\frac{1}{2}×1×FH$
=$\frac{1}{2}(FG+HF)$.
∴$\frac{1}{2}(FG+HF)$=$\frac{\sqrt{2}}{4}$.
∴FG+HF=$\frac{\sqrt{2}}{2}$
∴$y=-x+\frac{{\sqrt{2}}}{2}$;
(3)如图3:过点G作GM⊥HF,垂足为M.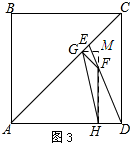
在四边形AGFH中,∠GFH=360°-∠GAH-∠FGA-∠FHA
=360°-45°-90°-90°
=135°
∴∠MFG=45°.
∴在Rt△GMF中,$\frac{GM}{GF}=\frac{\sqrt{2}}{2}$,即$\frac{GM}{x}=\frac{\sqrt{2}}{2}$,
∴GM=$\frac{{\sqrt{2}}}{2}x$
∴S△GFH$\frac{1}{2}GM•FH=\frac{1}{2}×\frac{\sqrt{2}}{2}x(-x+\frac{\sqrt{2}}{2})$=$-\frac{\sqrt{2}}{4}(x-\frac{\sqrt{2}}{4})^{2}+\frac{\sqrt{2}}{32}$.
∴△GHF面积的最大值为$\frac{{\sqrt{2}}}{32}$.
点评 本题主要考查的是相似三角形的性质和判定和函数知识的综合应用,面积法和配方法求二次函数最值的应用是解题的关键.

 寒假学与练系列答案
寒假学与练系列答案| A. | (-3,0) | B. | (-2,0) | C. | (-1,0) | D. | (3,0) |
| 薄板的边长(cm) | 20 | 30 |
| 出厂价(元/张) | 50 | 70 |
(2)若一张薄板的利润是34元,且成本最低,此时薄板的边长为多少?
(3)若限定薄板的边长不超过20cm,浮动价下降a%,其他条件不变,薄板的利润随边长的增加而增大时,直接写出a的取值范围.
 如图,直线AB,CD被BC所截,E是BC上一点,连接DE.若AB∥CD,∠1=45°,∠2=35°,则∠3=80度.
如图,直线AB,CD被BC所截,E是BC上一点,连接DE.若AB∥CD,∠1=45°,∠2=35°,则∠3=80度.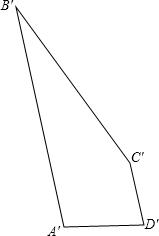 如图所示,四边形A′B′C′D′是将四边形ABCD平移后得到的,已知A′B′=13,B′C′=12,C′D′=3,D′A′=4,求四边形ABCD的周长.
如图所示,四边形A′B′C′D′是将四边形ABCD平移后得到的,已知A′B′=13,B′C′=12,C′D′=3,D′A′=4,求四边形ABCD的周长.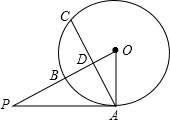 如图,已知PA为⊙O的切线,点A为切点,PO交⊙O于点B,点C是⊙O上一点,且$\widehat{AB}$=$\widehat{BC}$,PO交AC于点D,若PA=2$\sqrt{6}$,OD=2,求⊙O的半径和BD的长.
如图,已知PA为⊙O的切线,点A为切点,PO交⊙O于点B,点C是⊙O上一点,且$\widehat{AB}$=$\widehat{BC}$,PO交AC于点D,若PA=2$\sqrt{6}$,OD=2,求⊙O的半径和BD的长.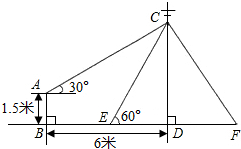 如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面成60°角,在离电线杆6米的B处安置测角仪,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长(结果保留根号).
如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面成60°角,在离电线杆6米的B处安置测角仪,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长(结果保留根号).