题目内容
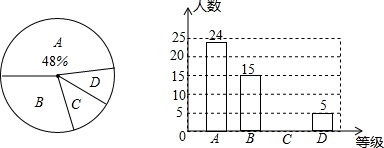
14.抛物线y=x2-2x+1向左平移2个单位长度后,所得到的抛物线与x轴的交点坐标为( )| A. | (-3,0) | B. | (-2,0) | C. | (-1,0) | D. | (3,0) |
分析 先把抛物线解析式整理出顶点式形式,从而确定出抛物线与x轴只有一个交点,再根据向左平移横坐标减,纵坐标不变求出平移后的抛物线顶点坐标,即为所求的点.
解答 解:∵y=x2-2x+1=(x-1)2,
∴抛物线顶点坐标为(1,0),
∵抛物线y=x2-2x+1向左平移2个单位长度,
∴平移后的抛物线顶点坐标为(-1,0),
即所得到的抛物线与x轴的交点坐标为(-1,0).
故选C.
点评 本题考查了二次函数图象与几何变换,要求熟练掌握平移的规律:左加右减,上加下减.并用规律求函数解析式,本题巧妙之处在于抛物线顶点坐标在x轴上.

练习册系列答案
相关题目
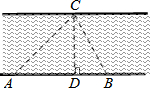 如图,为测量一段两岸互相平行的护城河的宽度CD,在河岸边选取A点与B点,测得∠CAB=45°,∠CBA=60°,AB=24m,求这段护城河的宽度CD.($\sqrt{3}$≈1.73,结果精确到1m.)
如图,为测量一段两岸互相平行的护城河的宽度CD,在河岸边选取A点与B点,测得∠CAB=45°,∠CBA=60°,AB=24m,求这段护城河的宽度CD.($\sqrt{3}$≈1.73,结果精确到1m.)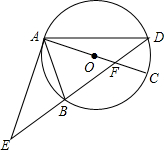 如图,⊙O的直径AC与弦BD相交于点F,点E是DB延长线上的一点,∠EAB=∠ADB.
如图,⊙O的直径AC与弦BD相交于点F,点E是DB延长线上的一点,∠EAB=∠ADB.
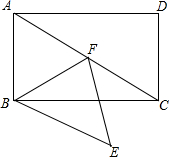 如图,点F在?ABCD的对角线AC上,过点F、B分别作AB、AC的平行线相交于点E,连接BF,∠ABF=∠FBC+∠FCB.
如图,点F在?ABCD的对角线AC上,过点F、B分别作AB、AC的平行线相交于点E,连接BF,∠ABF=∠FBC+∠FCB.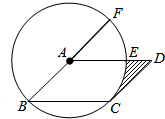 如图,在?ABCD中,以点A为圆心,AB的长为半径的圆恰好与CD相切于点C,交AD于点E,延长BA与⊙O相交于点F.若$\widehat{EF}$的长为$\frac{π}{2}$,则图中阴影部分的面积为2-$\frac{π}{2}$.
如图,在?ABCD中,以点A为圆心,AB的长为半径的圆恰好与CD相切于点C,交AD于点E,延长BA与⊙O相交于点F.若$\widehat{EF}$的长为$\frac{π}{2}$,则图中阴影部分的面积为2-$\frac{π}{2}$. 如图,∠1=∠2,∠C=∠D,找出图中与∠A相等的角,并说明理由.
如图,∠1=∠2,∠C=∠D,找出图中与∠A相等的角,并说明理由.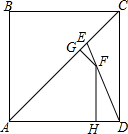 如图,已知正方形ABCD的边长为1,对角线AC上有一点E,使得AE=$\frac{{\sqrt{2}}}{2}$AC.连结DE,过线段DE上的一个动点F分别向AC和AD作垂线段,垂足分别为G、H.
如图,已知正方形ABCD的边长为1,对角线AC上有一点E,使得AE=$\frac{{\sqrt{2}}}{2}$AC.连结DE,过线段DE上的一个动点F分别向AC和AD作垂线段,垂足分别为G、H.