Question

16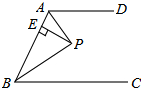．如图，AD∥BC，∠ABC的平分线BP与∠BAD的平分线AP相交于点P，作PE⊥AB于点E，若PE=3，则两平行线AD与BC间的距离为（　　）

• A． 3
• B． 4
• C． 5
• D． 6

Answer 1

分析 过点P作PF⊥AD于F，作PG⊥BC于G，根据角平分线上的点到角的两边距离相等可得PF=PE，PG=PE，再根据平行线之间的距离的定义判断出EG的长即为AD、BC间的距离．

解答 解：如图，过点P作PF⊥AD于F，作PG⊥BC于G，
∵AP是∠BAD的平分线，PE⊥AB，
∴PF=PE，
同理可得PG=PE，
∵AD∥BC，
∴点F、P、G三点共线，
∴EG的长即为AD、BC间的距离，
∴平行线AD与BC间的距离为3+3=6，
故选D．

点评 本题考查了角平分线上的点到角的两边距离相等的性质，平行线间的距离的定义，熟记性质并作辅助线构造出AD、BC间的距离的线段是解题的关键．