题目内容
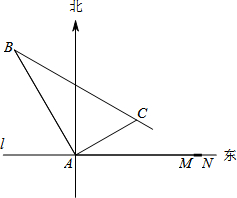 在某飞机场东西方向的地面l上有一长为1km的飞机跑道MN(如图),在跑道MN的正西端14.5千米处有一观察站A.某时刻测得一架匀速直线降落的飞机位于点A的北偏西30°,且与点A相距15千米的B处;经过1分钟,又测得该飞机位于点A的北偏东60°,且与点A相距5
在某飞机场东西方向的地面l上有一长为1km的飞机跑道MN(如图),在跑道MN的正西端14.5千米处有一观察站A.某时刻测得一架匀速直线降落的飞机位于点A的北偏西30°,且与点A相距15千米的B处;经过1分钟,又测得该飞机位于点A的北偏东60°,且与点A相距5| 3 |
(1)该飞机航行的速度是多少千米/小时?(结果保留根号)
(2)如果该飞机不改变航向继续航行,那么飞机能否降落在跑道MN之间?请说明理由.
考点:解直角三角形的应用-方向角问题
专题:
分析:(1)先求出∠BAC=90°,然后利用勾股定理列式求解即可得到BC,再求解即可;
(2)作CE⊥l于E,设直线BC交l于F,然后求出CE、AE,然后求出AF的长,再进行判断即可.
(2)作CE⊥l于E,设直线BC交l于F,然后求出CE、AE,然后求出AF的长,再进行判断即可.
解答:解:(1)由题意,得∠BAC=90°,
∴BC=
=10
,
∴飞机航行的速度为:10
×60=600
(km/h);
(2)能;
作CE⊥l于点E,设直线BC交l于点F.
在Rt△ABC中,AC=5
,BC=10
,
∴∠ABC=30°,即∠BCA=60°,
又∵∠CAE=30°,∠ACE=∠FCE=60°,
∴CE=AC•sin∠CAE=
,
AE=AC•cos∠CAE=
.
则AF=2AE=15(km),
∴AN=AM+MN=14.5+1=15.5km,
∵AM<AF<AN,
∴飞机不改变航向继续航行,可以落在跑道MN之间.

∴BC=
152+(5
|
| 3 |
∴飞机航行的速度为:10
| 3 |
| 3 |
(2)能;
作CE⊥l于点E,设直线BC交l于点F.
在Rt△ABC中,AC=5
| 3 |
| 3 |
∴∠ABC=30°,即∠BCA=60°,
又∵∠CAE=30°,∠ACE=∠FCE=60°,
∴CE=AC•sin∠CAE=
| 5 |
| 2 |
| 3 |
AE=AC•cos∠CAE=
| 15 |
| 2 |
则AF=2AE=15(km),
∴AN=AM+MN=14.5+1=15.5km,
∵AM<AF<AN,
∴飞机不改变航向继续航行,可以落在跑道MN之间.
点评:本题考查了解直角三角形的应用,方向角的定义,勾股定理,读懂题目信息并作出辅助线构造成直角三角形是解题的关键.

练习册系列答案
相关题目
某农场各用10块面积相同的试验田种植甲/乙两种大豆,收成后对两种大豆产量(单位:吨/亩)的数据统计如下:
≈0.54,
≈0.5,S2甲≈0.01,S2乙≈0.002,则由上述数据推断乙种大豆产量比较稳定的依据是( )
. |
| x甲 |
. |
| x乙 |
A、
| ||||
| B、S2甲>S2乙 | ||||
C、
| ||||
D、
|
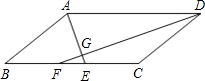 如图,在平行四边形ABCD中,∠BAD,∠ADC的平分线AE,DF分别与线段BC相交于点E,F,AE与DF相交于点G.
如图,在平行四边形ABCD中,∠BAD,∠ADC的平分线AE,DF分别与线段BC相交于点E,F,AE与DF相交于点G.
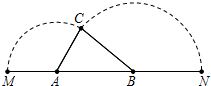 如图,已知A、B是线段MN上的两点,MN=4,MA=1,MB>1.以A为中心顺时针旋转点M,以B为中心逆时针旋转点N,使M、N两点重合成一点C,构成△ABC,设AB=x.
如图,已知A、B是线段MN上的两点,MN=4,MA=1,MB>1.以A为中心顺时针旋转点M,以B为中心逆时针旋转点N,使M、N两点重合成一点C,构成△ABC,设AB=x.