题目内容
14.已知多项式x3-3xy2-4的常数项是a,次数是b(1)直接写出a,b,并将这两个数在数轴上所对应的点A、B表示出来;
(2)数轴上A、B之间的距离记作|AB|,定义:|AB|=|a-b|,设点P在数轴上对应的数为x,当|PA|+|PB|=13时,直接写出x的值6或-7;
(3)若点A、点B同时沿数轴向正方向运动,点A的速度是点B的2倍,且3秒后,$\frac{3}{2}$AO=OB,求点B的速度.
分析 (1)根据多项式中常数项及多项式的次数的定义即可求解;
(2)根据|PA|+|PB|=13列出方程,解方程即可;
(3)设点B的速度为v,则A的速度为2v,分A在原点O的左边与A在原点O的右边进行讨论.
解答 解:(1)∵多项式x3-3xy2-4的常数项是a,次数是b,
∴a=-4,b=3,
点A、B在数轴上如图所示:
(2)根据题意得
|x-(-4)|+|x-3|=13,
点P在A点左边,-x-4-x+3=13,解得x=-7;
点P在A点右边,x+4+x-3=13,解得x=6.
故x的值为6或-7;
(3)设B速度为v,则A的速度为2v,3秒后点,A点在数轴上表示的数为(-4+6v),B点在数轴上表示的数为3+3v,
当A还在原点O的左边时,由$\frac{3}{2}$OA=OB可得$\frac{3}{2}$(4-6v)=3+3v,解得v=$\frac{1}{4}$;
当A在原点O的右边时,由$\frac{3}{2}$OA=OB可得$\frac{3}{2}$(6v-4)=3+3v,v=$\frac{3}{2}$.
故点B的速度为$\frac{1}{4}$或$\frac{3}{2}$.
故答案为:6或-7.
点评 本题考查了一元一次方程的应用与数轴,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.

练习册系列答案
相关题目
4. 如图,将长8cm,宽4cm的矩形纸片ABCD折叠,使点A与C重合,则四边形AECF的周长为( )
如图,将长8cm,宽4cm的矩形纸片ABCD折叠,使点A与C重合,则四边形AECF的周长为( )
 如图,将长8cm,宽4cm的矩形纸片ABCD折叠,使点A与C重合,则四边形AECF的周长为( )
如图,将长8cm,宽4cm的矩形纸片ABCD折叠,使点A与C重合,则四边形AECF的周长为( )| A. | 12 cm | B. | 16 cm | C. | 20 cm | D. | 24 cm |
9. 小龙在学校组织的社会调查活动中负责了解他所居住的小区440户居民的家庭收入情况.他从中随机调查了40户居民家庭的人均月收入(收入取整数,单位:元),并绘制了频数分布表和频数分布直方图(如图).根据以上信息,解答下列问题:
小龙在学校组织的社会调查活动中负责了解他所居住的小区440户居民的家庭收入情况.他从中随机调查了40户居民家庭的人均月收入(收入取整数,单位:元),并绘制了频数分布表和频数分布直方图(如图).根据以上信息,解答下列问题:
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
(2)如果家庭人均月收入“大于1000不足1600元”的为中等收入家庭,请你通过样本估计总体中的中等收入家庭大约有多少户?
 小龙在学校组织的社会调查活动中负责了解他所居住的小区440户居民的家庭收入情况.他从中随机调查了40户居民家庭的人均月收入(收入取整数,单位:元),并绘制了频数分布表和频数分布直方图(如图).根据以上信息,解答下列问题:
小龙在学校组织的社会调查活动中负责了解他所居住的小区440户居民的家庭收入情况.他从中随机调查了40户居民家庭的人均月收入(收入取整数,单位:元),并绘制了频数分布表和频数分布直方图(如图).根据以上信息,解答下列问题:| 分组 | 频数 | 频率 |
| 600~799 | 2 | 0.050 |
| 800~999 | 6 | 0.150 |
| 1000~1199 | 18 | 0.450 |
| 1200~1399 | 9 | 0.225 |
| 1400~1599 | 3 | 0.075 |
| 1600~1800 | 2 | 0.050 |
| 合计 | 40 | 1.000 |
(2)如果家庭人均月收入“大于1000不足1600元”的为中等收入家庭,请你通过样本估计总体中的中等收入家庭大约有多少户?

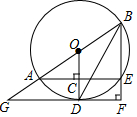 已知,如图,AB是⊙O的直径,AE是⊙O的弦,过点O作⊙O的半径OD⊥AE于点C,延长交⊙O于点D,连BE并延长,过点D作DF⊥BE于点F,交BA的延长线于点G.
已知,如图,AB是⊙O的直径,AE是⊙O的弦,过点O作⊙O的半径OD⊥AE于点C,延长交⊙O于点D,连BE并延长,过点D作DF⊥BE于点F,交BA的延长线于点G.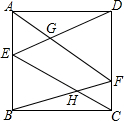 如图,正方形ABCD的面积为4,E,F分别是AB、CD上的点,AF与ED相交于点G,BF与EC相交于点H,求四边形EHFG面积的最大值.
如图,正方形ABCD的面积为4,E,F分别是AB、CD上的点,AF与ED相交于点G,BF与EC相交于点H,求四边形EHFG面积的最大值.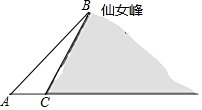 数学“综合与实践”课中,老师带领同学们来到娄底市郊区,测算如图所示的仙女峰的高度,李红盛同学利用已学的数学知识设计了一个实践方案,并实施了如下操作:先在水平地面A处测得山顶B的仰角∠BAC为38.7°,再由A沿水平方向前进377米到达山脚C处,测得山坡BC的坡度为1:0.6,请你求出仙女峰的高度(参考数据:tan38.7°≈0.8)
数学“综合与实践”课中,老师带领同学们来到娄底市郊区,测算如图所示的仙女峰的高度,李红盛同学利用已学的数学知识设计了一个实践方案,并实施了如下操作:先在水平地面A处测得山顶B的仰角∠BAC为38.7°,再由A沿水平方向前进377米到达山脚C处,测得山坡BC的坡度为1:0.6,请你求出仙女峰的高度(参考数据:tan38.7°≈0.8)