题目内容
9. 小龙在学校组织的社会调查活动中负责了解他所居住的小区440户居民的家庭收入情况.他从中随机调查了40户居民家庭的人均月收入(收入取整数,单位:元),并绘制了频数分布表和频数分布直方图(如图).根据以上信息,解答下列问题:
小龙在学校组织的社会调查活动中负责了解他所居住的小区440户居民的家庭收入情况.他从中随机调查了40户居民家庭的人均月收入(收入取整数,单位:元),并绘制了频数分布表和频数分布直方图(如图).根据以上信息,解答下列问题:| 分组 | 频数 | 频率 |
| 600~799 | 2 | 0.050 |
| 800~999 | 6 | 0.150 |
| 1000~1199 | 18 | 0.450 |
| 1200~1399 | 9 | 0.225 |
| 1400~1599 | 3 | 0.075 |
| 1600~1800 | 2 | 0.050 |
| 合计 | 40 | 1.000 |
(2)如果家庭人均月收入“大于1000不足1600元”的为中等收入家庭,请你通过样本估计总体中的中等收入家庭大约有多少户?
分析 (1)根据直方图可得到1400~1599范围内的人数,然后根据频率=频数÷数据个数可求得其频率,然后依据总数等于各部分的和可求得1000~1199的频数;
(2)先求得样本中大于1000不足1600元家庭所占的百分比,然后用样本故此总体即可.
解答 解:(1)直方图可知第5小组有3人,频率=3÷40=0.075.
40-2-6-9-3-2=18,第3小组的频数为18.
故答案为18,3,0.075.
补全统计表和统计图如下
| 分组 | 频数 | 频率 |
| 600~799 | 2 | 0.050 |
| 800~999 | 6 | 0.150 |
| 1000~1199 | 18 | 0.450 |
| 1200~1399 | 9 | 0.225 |
| 1400~1599 | 3 | 0.075 |
| 1600~1800 | 2 | 0.050 |
| 合计 | 40 | 1.000 |

(2)(18+9+3)÷40×440=330.
答:该小区440户居民的家庭中的中等收入家庭大约有330户.
点评 本题主要考查的是频数分布直方图和频数部分表的认识,掌握频数、频数、数据总数之间的关系是解题的关键.

练习册系列答案
相关题目
20.某工厂生产一种合金薄板(其厚度忽略不计),这些薄板的形状均为正方形,边长(单位:cm)在5~50(含5和50)之间,每张薄板的成本价(单位:元)与它的面积(单位:cm2)成正比例,每张薄板的出厂价(单位:元)由基础价和浮动价两部分组成,其中基础价与薄板的大小无关,是固定不变的,浮动价与薄板的边长成正比例,在营销过程中得到了表格中的数据:
(1)求一张薄板的出厂价y与边长x之间满足的函数关系式,并写出自变量的取值范围;
(2)已知出厂一张边长为40cm的薄板,获得利润是26元(利润=出厂价-成本价).
①求一张薄板的利润W与边长x这之间满足的函数关系式;
②当边长为多少厘米时,出厂一张薄板获得的利润最大?最大利润是多少元?
| 薄板的边长(cm) | 20 | 30 |
| 出厂价(元/张) | 50 | 70 |
(2)已知出厂一张边长为40cm的薄板,获得利润是26元(利润=出厂价-成本价).
①求一张薄板的利润W与边长x这之间满足的函数关系式;
②当边长为多少厘米时,出厂一张薄板获得的利润最大?最大利润是多少元?
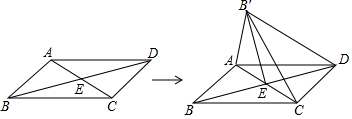
17.如图,在?ABCD中,对角线AC与BD相交于点E,∠AEB=45°,BD=4,将△ABC沿直线AC翻折180°后与原图形在同一平面内,若点B的落点记为B′,则DB′的长为( )

| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 4$\sqrt{2}$ | D. | $\sqrt{5}$ |
19.若关于x的一元二次方程kx2-4x+1=0有实数根,则k的取值范围是( )
| A. | k=4 | B. | k>4 | C. | k≤4且k≠0 | D. | k≤4 |
 如图,BD是△ABC的角平分线,点E、F分别在BC、AB上,且DE∥AB,EF∥AC.
如图,BD是△ABC的角平分线,点E、F分别在BC、AB上,且DE∥AB,EF∥AC.