题目内容
6.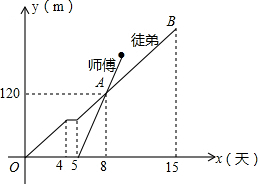 为了检修自来水管道,由师徒两人完成,两人从管道两端开始检修,已知徒弟先修了4天后,休息了1天,接着师徒两人合做了5天,师傅被安排做其他工作,余下由徒弟单独检修完,如图是师傅和徒弟修管道的长度与工作时间的函数图象,请根据图象提供的信心解答下列问题.
为了检修自来水管道,由师徒两人完成,两人从管道两端开始检修,已知徒弟先修了4天后,休息了1天,接着师徒两人合做了5天,师傅被安排做其他工作,余下由徒弟单独检修完,如图是师傅和徒弟修管道的长度与工作时间的函数图象,请根据图象提供的信心解答下列问题.(1)点A的实际意义;
(2)求直线AB的函数关系式;
(3)这个自来水管道共有多少米?
分析 (1)点A是两函数图象的交点,表示徒弟工作7天完成的工作量与师父工作3天完成的工作量相同;
(2)先求出B点坐标为(15,240),再设直线AB的函数关系式为y=kx+b,利用待定系数法即可求解;
(3)先求出师父工作5天完成的米数,再加上240,即可求解.
解答 解:(1)点A是两函数图象的交点,表示徒弟工作7天完成的工作量与师父工作3天完成的工作量相同;
(2)∵徒弟工作7天完成120m,
∴徒弟的工作效率是$\frac{120}{7}$m/天,
∴徒弟工作14天完成14×$\frac{120}{7}$=240m,
∴B(15,240).
设直线AB的函数关系式为y=kx+b,
∵A(8,120),B(15,240),
∴$\left\{\begin{array}{l}{8k+b=120}\\{15k+b=240}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{120}{7}}\\{b=-\frac{120}{7}}\end{array}\right.$,
∴直线AB的函数关系式为y=$\frac{120}{7}$x-$\frac{120}{7}$;
(3)∵师父工作3天完成120m,
∴师父的工作效率是40m/天,
∴师父工作5天完成40×5=200m,
∵徒弟一共完成240m,
∴这个自来水管道共有200+240=440米.
点评 本题考查了一次函数的应用,点的坐标的运用,待定系数法求一次函数的解析式的运用,工作总量=工作效率×工作时间的运用.解答时求出解析式是关键.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
16.不等式组$\left\{\begin{array}{l}{2x+1>3}\\{3x-5≤1}\end{array}\right.$的解集是( )
| A. | x>2 | B. | x<1 | C. | 1<x≤2 | D. | 无解 |
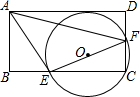 如图,矩形ABCD中,E为BC上一点,F为CD上一点,已知∠AEF=90°,$\frac{AE}{EF}$=$\frac{3}{4}$,△ECF的外接圆与AD相切,则tan∠DAF=$\frac{16}{63}$.
如图,矩形ABCD中,E为BC上一点,F为CD上一点,已知∠AEF=90°,$\frac{AE}{EF}$=$\frac{3}{4}$,△ECF的外接圆与AD相切,则tan∠DAF=$\frac{16}{63}$.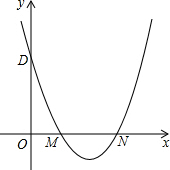 抛物线y=x2-4x+3交x轴于M,N点(M点在N点左边),交y轴于D点,点E为第一象限抛物线上的点,若∠EMN=2∠ODM,求E点坐标.
抛物线y=x2-4x+3交x轴于M,N点(M点在N点左边),交y轴于D点,点E为第一象限抛物线上的点,若∠EMN=2∠ODM,求E点坐标. 如图,已知点A(1,2)是函数y=$\frac{2}{x}$(x>0)的图象的点,连结OA,作OA⊥0B,与图象y=$\frac{-6}{x}$(x>0)交于点B.
如图,已知点A(1,2)是函数y=$\frac{2}{x}$(x>0)的图象的点,连结OA,作OA⊥0B,与图象y=$\frac{-6}{x}$(x>0)交于点B. 如图,将一张长方形纸片的一角斜折过去,使角的顶点A落在A′处,BC为折痕,若BD平分∠A′BE,则BC与BD的位置关系是垂直.
如图,将一张长方形纸片的一角斜折过去,使角的顶点A落在A′处,BC为折痕,若BD平分∠A′BE,则BC与BD的位置关系是垂直. 甲、乙两人同时从相距90千米的A地前往B地,甲乘汽车,乙骑摩托车匀速行驶(汽车速度大于摩托车的速度);甲先到达B地停留半个小时后返回A地,如图是他们之间的距离y(千米)与甲出发时间x(小时)之间的函数图象,其中D表示甲返回到A地.
甲、乙两人同时从相距90千米的A地前往B地,甲乘汽车,乙骑摩托车匀速行驶(汽车速度大于摩托车的速度);甲先到达B地停留半个小时后返回A地,如图是他们之间的距离y(千米)与甲出发时间x(小时)之间的函数图象,其中D表示甲返回到A地.