题目内容
4．试证明：无论m取何实数，关于x（的方程（m2-8m+17）x2+2m+1=0都是一元二次方程．分析 利用配方法得出（m-4）2+1＞0，进而得出答案．
解答 证明：∵m2-8m+17=（m-4）2+1，
∴（m-4）2+1＞0，
∴关于x（的方程（m2-8m+17）x2+2m+1=0都是一元二次方程．
点评 此题主要考查了一元二次方程的定义，正确配方是解题关键．
练习册系列答案
相关题目
14．下列运算正确的是（ ）
| A． | （ab）2=ab2 | B． | 3a+2a2=5a2 | C． | 2（a+b）=2a+b | D． | a•a=a2 |
15．
如图，AOB是一条直线，∠AOD=∠EOC=∠DOB=90°，那么互为补角的角共有（ ）
如图，AOB是一条直线，∠AOD=∠EOC=∠DOB=90°，那么互为补角的角共有（ ）| A． | 3对 | B． | 4对 | C． | 6对 | D． | 7对 |
9．化简$\sqrt{2}$+（$\sqrt{2}$-1）的结果是（ ）
| A． | $2\sqrt{2}-1$ | B． | $2-\sqrt{2}$ | C． | $1-\sqrt{2}$ | D． | $2+\sqrt{2}$ |
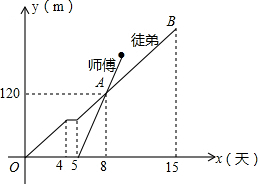为了检修自来水管道，由师徒两人完成，两人从管道两端开始检修，已知徒弟先修了4天后，休息了1天，接着师徒两人合做了5天，师傅被安排做其他工作，余下由徒弟单独检修完，如图是师傅和徒弟修管道的长度与工作时间的函数图象，请根据图象提供的信心解答下列问题．